Next: Implementazione in Matlab Up: Fattorizzazione Previous: Fattorizzazione Indice
Se, per esempio, avessimo che
![]() con il metodo
precedente non potremmo proseguire, ma siamo sicuri che
all'interno della stessa colonna esiste un elemento non nullo
(altrimenti avremmo una colonna tutta nulla che comporterebbe la
singolarità della matrice, in opposizione alle ipotesi). Cerchiamo
allora un altro elemento diverso da zero nel seguente modo,
limitandoci al caso reale:
con il metodo
precedente non potremmo proseguire, ma siamo sicuri che
all'interno della stessa colonna esiste un elemento non nullo
(altrimenti avremmo una colonna tutta nulla che comporterebbe la
singolarità della matrice, in opposizione alle ipotesi). Cerchiamo
allora un altro elemento diverso da zero nel seguente modo,
limitandoci al caso reale:
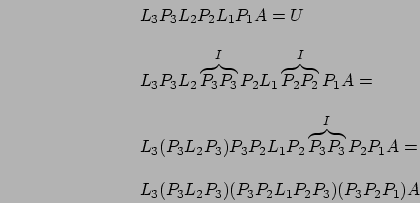 ) che scambia la prima riga con la k1-esima:
) che scambia la prima riga con la k1-esima:
Dopo aver costruito la matrice di permutazione elementare,
possiamo eseguire 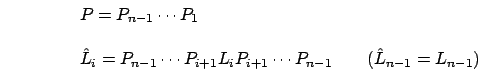 che scambia nella matrice
che scambia nella matrice ![]() le
righe
le
righe ![]() e
e ![]() . Ristrutturata in questo modo, la matrice
. Ristrutturata in questo modo, la matrice
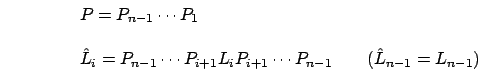 possiede tutti i requisiti richiesti dal metodo di
eliminazione di Gauss, che dunque possiamo applicare; ottenuta
dunque la matrice
possiede tutti i requisiti richiesti dal metodo di
eliminazione di Gauss, che dunque possiamo applicare; ottenuta
dunque la matrice ![]() come visto per l'algoritmo precedente,
portiamo a termine il primo passo ottenendo come risultato:
come visto per l'algoritmo precedente,
portiamo a termine il primo passo ottenendo come risultato:
Un fatto interessante da notare è che, calcolando il vettore
elementare di Gauss come già visto, e cioè come
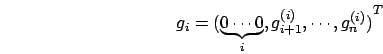 come il massimo della prima colonna, e
come favorevole conseguenza abbiamo che gli errori sono ben
limitati in aritmetica finita; questa considerazione è valida per
la matrice
come il massimo della prima colonna, e
come favorevole conseguenza abbiamo che gli errori sono ben
limitati in aritmetica finita; questa considerazione è valida per
la matrice
Quello che abbiamo descritto ora è il metodo di pivoting parziale,
in quanto viene scelto il pivot (l'elemento diagonale utilizzato
per costruire il vettore elementare di Gauss) non in modo statico
come avveniva per la fattorizzazione ![]() ma viene ricercato
all'interno della colonna in esame l'elemento di modulo massimo, e
con quello si procede con l'algoritmo di eliminazione di Gauss.
ma viene ricercato
all'interno della colonna in esame l'elemento di modulo massimo, e
con quello si procede con l'algoritmo di eliminazione di Gauss.
Ottenuta la matrice 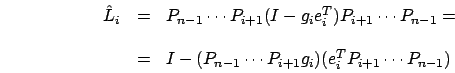 possiamo continuare ad applicare
l'algoritmo di scambio e di fattorizzazione. Ripetuto questo passo
per
possiamo continuare ad applicare
l'algoritmo di scambio e di fattorizzazione. Ripetuto questo passo
per ![]() volte otteniamo
volte otteniamo
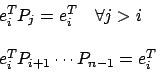
Abbiamo ottenuto la matrice ![]() , ma come possiamo ottenere
, ma come possiamo ottenere ![]() ?
Facciamo un esempio con
?
Facciamo un esempio con ![]() tenendo a mente che
tenendo a mente che ![]() è
simmetrica ed ortogonale:
è
simmetrica ed ortogonale:
In generale definiamo
Se le matrici 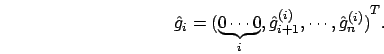 avessero la stessa struttura delle
matrici elementari di Gauss avremmo trovato la nostra
fattorizzazione poichè potremmo nuovamente definire
avessero la stessa struttura delle
matrici elementari di Gauss avremmo trovato la nostra
fattorizzazione poichè potremmo nuovamente definire
![]() per poi ottenere la
fattorizzazione
per poi ottenere la
fattorizzazione ![]() ; cerchiamo di verificare allora che
; cerchiamo di verificare allora che
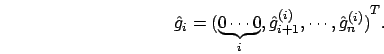 ed
ed ![]() hanno la stessa struttura: partendo dal
vettore elementare di Gauss
hanno la stessa struttura: partendo dal
vettore elementare di Gauss
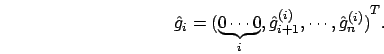
 applicato ad una matrice seleziona l'i-esima riga, ma
applicato ad una matrice seleziona l'i-esima riga, ma  ,
ad esempio, ha le prime
,
ad esempio, ha le prime
Ci siamo ridotti a
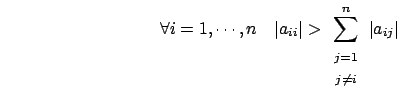 :
: 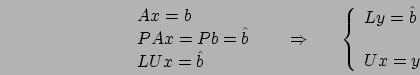 è la
matrice elementare di permutazione che scambia
è la
matrice elementare di permutazione che scambia 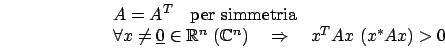 che applicata a
che applicata a 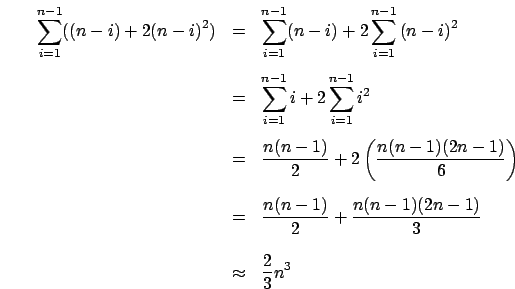 produce una permutazione degli
elementi del vettore dal'indice
produce una permutazione degli
elementi del vettore dal'indice 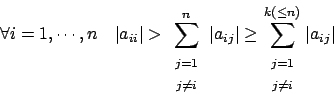
 ha prodotto un vettore con gli
elementi
ha prodotto un vettore con gli
elementi
Morpheus 2004-01-04