Questo dato ci indica quanto velocemente la successione di valori
generata da un metodo numerico converge verso la soluzione.
Considerando
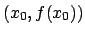 come l'errore relativo
commesso al passo
come l'errore relativo
commesso al passo 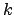 , si dice che un metodo ha convergenza
, si dice che un metodo ha convergenza
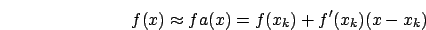 se e solo se:
se e solo se:
con 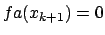 che è detta costate asintotica
dell'errore e rappresenta quanto è più piccolo
che è detta costate asintotica
dell'errore e rappresenta quanto è più piccolo 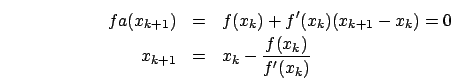 rispetto a
rispetto a 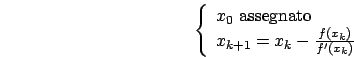 . E' utile notare che, nel caso
. E' utile notare che, nel caso 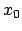 è
necessario che
è
necessario che  altrimenti il metodo non convergerebbe,
come si vede
altrimenti il metodo non convergerebbe,
come si vede
e se
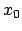 perché converga deve essere
perché converga deve essere 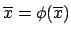 .
.
Nel caso del metodo si bisezione, il limite diviene
infatti ad ogni passo di dimezza il campo di ricerca. Il metodo di
bisezione è quello che si dice un metodo lineare (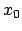 ), è lento
ma ha il pregio di avere un limite superiore al numero di
iterazioni necessarie per ottenere un'approssimazione della
soluzione ed in più converge sempre, ha quella che si chiama
convergenza totale: qualsiasi sia l'intervallo scelto, che
rispetti le ipotesi iniziali, il metodo di bisezione ci porterà
verso la soluzione; vedremo che questo comportamento non è comune
a tutti gli algoritmi.
), è lento
ma ha il pregio di avere un limite superiore al numero di
iterazioni necessarie per ottenere un'approssimazione della
soluzione ed in più converge sempre, ha quella che si chiama
convergenza totale: qualsiasi sia l'intervallo scelto, che
rispetti le ipotesi iniziali, il metodo di bisezione ci porterà
verso la soluzione; vedremo che questo comportamento non è comune
a tutti gli algoritmi.
Morpheus
2004-01-04
![]() come l'errore relativo
commesso al passo
come l'errore relativo
commesso al passo ![]() , si dice che un metodo ha convergenza
, si dice che un metodo ha convergenza
![]() se e solo se:
se e solo se: 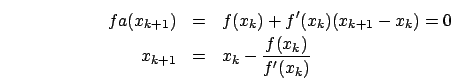 rispetto a
rispetto a 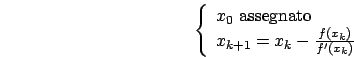 . E' utile notare che, nel caso
. E' utile notare che, nel caso