La seconda serie delle leggi dinamiche riguarda la
sequenzializzazione e si focalizza sul significato dell'azione
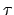
-
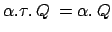
-
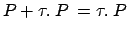
-
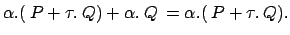
Queste leggi possono apparire strane ad un primo esame, ma andando
ad analizzare i relativi alberi di derivazione ci si può rendere
conto della correttezza di tali leggi. Per esempio una conseguenza
diretta delle 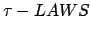 è la seguente uguaglianza:
Essa è facilmente dimostrabile usando la legge
è la seguente uguaglianza:
Essa è facilmente dimostrabile usando la legge  delle
delle
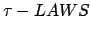 . Il menbro destro dell'uguaglianza, P, rappresenta la
capacità di compiere azioni inizialmente possibili ma che
rimangono tali anche dopo l'azione
. Il menbro destro dell'uguaglianza, P, rappresenta la
capacità di compiere azioni inizialmente possibili ma che
rimangono tali anche dopo l'azione 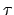 , in pratica le
possibilità del sistema restano immutate anche posticipando le
azioni di P dopo l'azione
, in pratica le
possibilità del sistema restano immutate anche posticipando le
azioni di P dopo l'azione 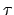 .
.
Queste sono le uniche leggi valide per l'azione 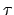 , se
ammettessimo la "legge"
, se
ammettessimo la "legge"
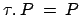 comporterebbe la seguente
uguaglianza:
comporterebbe la seguente
uguaglianza:
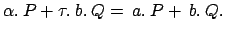 ; questo
comporterebbe un'errore perchè se il membro sinistro compie
l'azione
; questo
comporterebbe un'errore perchè se il membro sinistro compie
l'azione 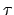 non sara più possibile compiere l'azione
non sara più possibile compiere l'azione 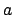 ,
possibilità che il membro destro non possiede.
,
possibilità che il membro destro non possiede.
Morpheus
2004-02-10
![]() , se
ammettessimo la "legge"
, se
ammettessimo la "legge"
![]() comporterebbe la seguente
uguaglianza:
comporterebbe la seguente
uguaglianza:
![]() ; questo
comporterebbe un'errore perchè se il membro sinistro compie
l'azione
; questo
comporterebbe un'errore perchè se il membro sinistro compie
l'azione ![]() non sara più possibile compiere l'azione
non sara più possibile compiere l'azione ![]() ,
possibilità che il membro destro non possiede.
,
possibilità che il membro destro non possiede.