Next: Nozioni preliminari di algebra Up: Semantica Operazionale di CCS Previous: LEGGI STATICHE Indice
Spesso un sistema concorrente viene definito tramite Composizione
parallela di molti processi sui quali viene effettuato un
Relabelling in modo che possano sincronizzarsi tra loro, per poi
applicare una Restrizione sull'insieme delle azioni di
sincronizzazione. L'espansione permette di elaborare le azioni di
questi ![]() e trasformare la descrizione del sistema in una
sommatoria di termini del tipo
e trasformare la descrizione del sistema in una
sommatoria di termini del tipo
![]() (Standard
Concurrent Form).
(Standard
Concurrent Form).
Le azioni manipolare sono di due tipi: quelle delle singole componenti e quelle che diventano azioni interne perché derivano da una comunicazione tra due processi.
Sia
![]() allora:
allora:
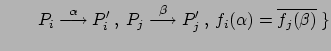 |
Diamo adesso la versione senza l'operazione di relabelling:
![]() allora:
allora:
Vediamo un semplice esempio in cui può essere molto utile la legge di espansione:
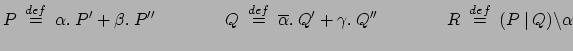
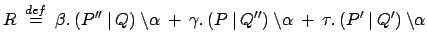
| BILL_BEN |
|
|
| BILL_BEN |
|
|
|
|
||
| BILL_BEN |
|
|
Nell'ultimo passaggio si è immediatamente trasformato
![]() nel semplice processo
inattivo
nel semplice processo
inattivo ![]() .
.
Morpheus 2004-02-10