Relazioni, preordini ed equivalenze

Definizione 4..1 (Relazione (binaria))   Una relazione $\mathcal{R}$ da un insieme $\mathcal{A}$ in un insieme $\mathcal{B}$ è un sottoinsieme del prodotto cartesiano dei due insiemi, cioè

$$\mathcal{R}: \mathcal{A} \rightarrow \mathcal{B} \subseteq \mathcal{A} \times \mathcal{B}$$

Per una relazione possono essere verificate alcune proprietà:

Definizione 4..2 (Proprietà delle relazioni)   Sia $\mathcal{R}$ una relazione da $\mathcal{A}$ in $\mathcal{A}$, allora si dice che $\mathcal{R}$ è

riflessiva

sse $\forall x \: \in \: \mathcal{A}$, implica $(x,x) \: \in \: \mathcal{R}$

transitiva

sse $\forall x,y,z \: \in \: \mathcal{A}$, $(x,y) \: \in \: \mathcal{R}$ e $(y,z) \: \in \: \mathcal{R}$ implica $(x,z) \: \in \: \mathcal{R}$

simmetrica

sse $\forall x,y \: \in \: \mathcal{A}$, $(x,y) \: \in \: \mathcal{R}$ implica $(y,x) \: \in \: \mathcal{R}$

antisimmetrica

sse $\forall x,y \: \in \: \mathcal{A}$, $(x,y) \: \in \: \mathcal{R}$ e $(y,x) \: \in \: \mathcal{R}$ implica $x=y$

Introduciamo la nozione di inversa di una relazione $\mathcal{R}$ e di composizione di due relazioni $\mathcal{R}_1$ e $\mathcal{R}_2$

$$\begin{array}{rcl} \par \mathcal{R}^{-1} & = & \{ (y,x): \:... ... \in \: \mathcal{R}_2 \mbox{ per qualche } y \} \end{array}$$

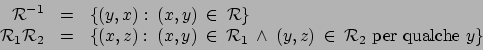
Alcune relazioni , che possiedono determinate proprietà, vengono chiamate in modo caratterizzante; definiamo infatti:

Definizione 4..3 (Equivalenza)   Una relazione binaria $\mathcal{R}$ su un insieme $\mathcal{A}$ è chiamata relazione di equivalenza se è riflessiva, simmetrica e transitiva.

Definizione 4..4 (Preordine)   Una relazione binaria $\mathcal{R}$ su un insieme $\mathcal{A}$ è chiamata preordine se è riflessiva e transitiva.

Solitamente i preordini vengono indicati con il simbolo $\sqsubseteq$; essendo una relazione, è possibile trovare l'inverso di un preordine, e ciò ci consente di definire

Definizione 4..5 (Kernel di un preordine)   Dato il preordine $\sqsubseteq$, definiamo il kernel del preordine come il preordine stesso intersecato con la relazione inversa, cioè $\simeq \: =\: \sqsubseteq \cap \sqsubseteq^{-1}$.

Questa operazione equivale a fare la chiusura simmetrica del preordine, ottenendo così una relazione di equivalenza. Questa possibilità di generare in modo molto diretto una relazione di equivalenza da un preordine ci sarà molto utile in seguito.