Next: Operatori Up: Algebre di Processi Previous: Labelled Transition Systems Indice
Un'azione rappresenta un passo di computazione che viene fatto da un sistema per poter andare da uno stato all'altro. Nella maggior parte delle teorie algebriche, le azioni costituiscono un'interazione con l'ambiente esterno tramite determinate porte del sistema, oppure rappresentano una computazione interna.
In genere un'azione si indica con lo stesso simbolo della porta su
cui agisce, perciò se denotiamo l'insieme delle porte nel
sistema considerato con il simbolo ![]() , si trova che
l'insieme di tutte le azioni visibili è il seguente:
, si trova che
l'insieme di tutte le azioni visibili è il seguente:
Questa transizione invisibile ha grande importanza nello studio
delle equivalenze tra sistemi perché può essere
considerata come quelle esterne oppure può avere un
trattamento proprio a seconda del tipo di equivalenza che si sta
analizzando. In questi ultimi casi si deve aggiungere la notazione
![]() che indica assenza di azioni visibili; quindi
che indica assenza di azioni visibili; quindi
![]() indica la possibilità di fare zero o più
azioni
indica la possibilità di fare zero o più
azioni ![]() (
(
![]() si utilizza quindi nello studio di
equivalenze di osservazione).
si utilizza quindi nello studio di
equivalenze di osservazione).
Dal momento che una transizione tra due stati è accompagnata
da un'azione, se dal processo ![]() si passa a
si passa a ![]() tramite
tramite
![]() , si parla di derivazione e si indica in
questo modo:
, si parla di derivazione e si indica in
questo modo:
Se per passare da un processo all'altro servono più azioni si
può anche utilizzare
![]() nella
derivazione.
nella
derivazione.
Nel caso in cui ci interessi il punto di vista di un osservatore
esterno, le azioni interne dovranno essere ignorate nelle
transizioni. Quindi si può avere la discendenza da P a Q
tramite l'azione visibile
![]() :
:
L'![]() -discendenza corrisponde alla derivazione di
-discendenza corrisponde alla derivazione di ![]() ,
ma preceduta e seguita da zero o più azioni interne, ovvero:
,
ma preceduta e seguita da zero o più azioni interne, ovvero:
Anche in questo caso possiamo utilizzare la sequenza di azioni
visibili
![]() .
.
L'
![]() -discendenza invece corrisponde alla derivazione di
zero o più
-discendenza invece corrisponde alla derivazione di
zero o più ![]() :
:
In alcuni casi può essere interessante soltanto la
capacità da parte del processo P di derivare o discendere
un'azione ![]() , mentre non ha importanza quale stato viene
raggiunto. Queste situazioni "più generiche" sono indicate nei
seguenti modi:
, mentre non ha importanza quale stato viene
raggiunto. Queste situazioni "più generiche" sono indicate nei
seguenti modi:
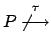 .
.
In alcune algebre di processi (tra le quali anche CCS) le azioni esterne si dividono in azioni di input e azioni di output.
Quando un processo esegue un'azione di input, significa che esso
riceve un segnale su una determinata porta ![]() ed in genere
si indica l'azione proprio con il simbolo
ed in genere
si indica l'azione proprio con il simbolo ![]() . Nel caso
dell'output, invece, è il processo stesso che emette il
segnale attraverso una porta
. Nel caso
dell'output, invece, è il processo stesso che emette il
segnale attraverso una porta ![]() ed in questo caso il simbolo
viene soprabarrato (
ed in questo caso il simbolo
viene soprabarrato (
![]() ).
).
![]() ed
ed
![]() sono dette azioni
complementari ed hanno un ruolo fondamentale nella comunicazione
tra due processi che agiscono in parallelo.
sono dette azioni
complementari ed hanno un ruolo fondamentale nella comunicazione
tra due processi che agiscono in parallelo.
Indicheremo con
![]() l'insieme delle azioni
complementari di
l'insieme delle azioni
complementari di ![]() , e con
, e con
![]() l'unione di questi due
insiemi:
l'unione di questi due
insiemi:
![]() . Inoltre, dato un
processo
. Inoltre, dato un
processo ![]() , si indicherà con
, si indicherà con
![]() l'insieme delle
azioni di
l'insieme delle
azioni di ![]() .
.
Esempio Bill-Ben
2: Riprendendo l'esempio introdotto per gli LTS, si osserva
facilmente che le azioni visibili sono ![]() e
e ![]() , mentre
l'unica azione interna del sistema è
, mentre
l'unica azione interna del sistema è ![]() . Se le azioni
visibili sono degli output, in alcune algebre (compresa CCS) si
scriverà
. Se le azioni
visibili sono degli output, in alcune algebre (compresa CCS) si
scriverà
![]() e
e
![]() .
.
Alcune derivazioni ovvie sono le seguenti:
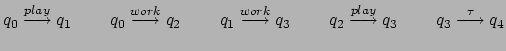
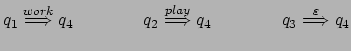
Morpheus 2004-02-10