Next: Caratterizzazione alternativa Up: Testing equivalence Previous: Testing equivalence Indice
Il comportamento esterno di programmi o processi, e più in generale di sistemi, può essere investigato tramite l'utilizzo di una serie di test. Risulta inoltre importante non soltanto sapere se, dato un particolare test, un processo risponde favorevolmente oppure no, ma anche se il processo risponde in maniera consistente ogni volta che il test viene eseguito.
Possiamo pensare, in generale, ad un insieme di processi e ad un insieme di test; due processi saranno equivalenti (rispetto a questo insieme di test) se superano esattamente gli stessi test. Questa naturale equivalenza può essere divisa in due preordini sui processi: il primo formulato in termini dell'abilità di rispondere positivamente ad un particolare test il secondo in termini dell'impossibilità di non rispondere positivamente ad un particolare test; nell'ultimo caso vedremo come un processo p sia meno di un processo q se, per ogni test a qui p risponde positivamente, anche q risponde positivamente. Attraverso la congiunzione di questi due preordini se ne otterrà un terzo, quello che caratterizza l'impianto teorico che stiamo discutendo.
Iniziamo dunque ad introdurre con maggior dettaglio quello di cui ci occuperemo:
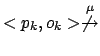 per ogni
per ogni
Come detto, un osservatore è un processo che esegue test su altri
processi comunicando con essi, in un certo senso guidandone
l'esecuzione. Un test su un processo avrà esito positivo se il suo
osservatore raggiunge uno stato in cui può eseguire l'azione ![]() ,
che comunica il successo.
,
che comunica il successo.
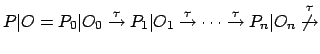
cioè una sequenza di transizioni ![]() o
o ![]() .
.
Un'osservazione si dice soddisfacente se
![]() , cioè se esiste uno stato in cui
l'osservatore è soddisfatto; questa definizione non implica
l'arresto dell'osservazione, ma richiede che si sia passati per
uno stato che consentiva di eseguire un'azione
, cioè se esiste uno stato in cui
l'osservatore è soddisfatto; questa definizione non implica
l'arresto dell'osservazione, ma richiede che si sia passati per
uno stato che consentiva di eseguire un'azione ![]()
Da quanto detto finora possiamo introdurre due concetti importanti per il proseguio:
La definizione sopra indica che un processo may satisfy un
osservatore se esiste un'osservazione soddisfacente per ![]() ,
mentre must satisfy un osservatore se tutte le osservazioni
per
,
mentre must satisfy un osservatore se tutte le osservazioni
per ![]() sono soddisfacenti.
sono soddisfacenti.
Con l'introduzione di may/must satisfy è possibile introdurre i tre preordini di questa teoria:
Definiti i preordini, prendendone il kernel, possiamo ottenere le relazioni di equivalenze corrispondenti:
Morpheus 2004-02-10