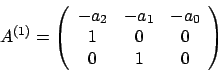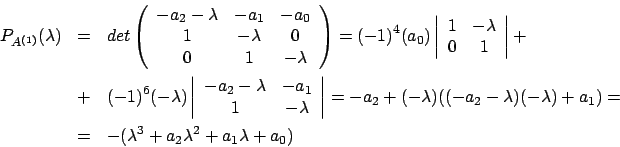Next: Implementazione in Matlab Up: Ricerca dell'autovalore dominante Previous: Ricerca dell'autovalore dominante Indice
Questo metodo è utilizzato proprio per risolvere il problema di
determinare l'autovalore dominante; a questo scopo viene richiesto
che
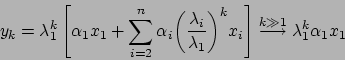
Il metodo procede come segue: dato
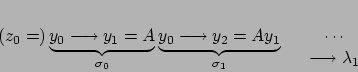

Con
 e sfruttando il fatto che
e sfruttando il fatto che ![]() è
dominante, si ottiene
è
dominante, si ottiene
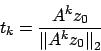
 tende ad allinearsi nella direzione
di
tende ad allinearsi nella direzione
di  , autovettore dominante.
, autovettore dominante.
Osserviamo adesso che
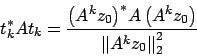
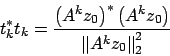
Questo algoritmo oltre all'autovalore dominante trova anche
l'autovettore associato, infatti  tende ad essere un
autovettore corrispondente a
tende ad essere un
autovettore corrispondente a ![]() .
.
Il metodo procede come segue:
Implementando così l'algoritmo potrebbe dare origine ad errori di
underflow ed overflow. Questi inconvenienti derivano dal fatto che
per calcolare ![]() dobbiamo calcolare
dobbiamo calcolare  e questo tende
a
e questo tende
a ![]() se
se
![]() mentre tende a
mentre tende a ![]() se
se
 ; l'underflow si può dire che sia un problema
"nascosto" poichè in quel caso
; l'underflow si può dire che sia un problema
"nascosto" poichè in quel caso
![]() ma poi si
vedrebbe che l'algoritmo non converge ad una approssimazione
accettabile.
ma poi si
vedrebbe che l'algoritmo non converge ad una approssimazione
accettabile.
Allora si cercano delle modifiche all'algoritmo per ovviare a
questi inconvenienti:
La successione adesso procede come segue:
Aver normalizzato il vettore ![]() rende
rende ![]() il
prodotto di una matrice per un vettore di norma uno che non
diventa mai troppo grande. Quello che interessa a noi è
un'approssimazione di
il
prodotto di una matrice per un vettore di norma uno che non
diventa mai troppo grande. Quello che interessa a noi è
un'approssimazione di ![]() ; si nota allora che
; si nota allora che
A partire da questi due valori si può scrivere
a questo punto siamo in grado di definite
 , che numericamente non danno problemi. A questo
punto il nuovo algoritmo è il seguente:
, che numericamente non danno problemi. A questo
punto il nuovo algoritmo è il seguente:
Come criteri di arresto possiamo prendere indifferentemente