Next: Il metodo delle potenze Up: Calcolo Numerico Previous: Conclusioni Indice
Data una matrice
![]() si dice
autovalore di
si dice
autovalore di ![]() ogni numero
ogni numero
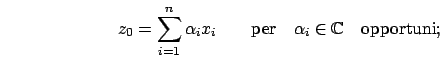 tale che
tale che
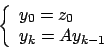
Come sappiamo (Teorema Rouche-Capelli) un sistema lineare omogeneo
ha soluzioni non nulle se e solo se la matrice dei coefficienti
del sistema è singolare e cioè ha determinante nullo; poichè
l'equazione precedente è equivalente al sistema
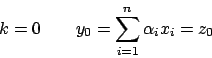
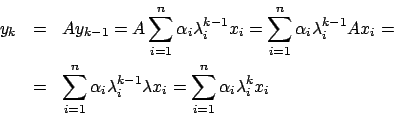
Calcolarsi gli autovalori risolvendo il polinomio caratteristico
comporta il calcolo del determinante di una matrice, un'operazione
molto costosa e spesso non necessaria. Esiste ad esempio il metodo
 che consente di calcolare l'intero spettro della matrice e
che genera una successione di matrici che trasformano per
similitudine la matrice data per ottenere una matrice triangolare
superiore. Dato il suo costo molto elevato e la complessità
dell'algoritmo non ce ne occuperemo, preferendo orientarci verso
un problema simile.
che consente di calcolare l'intero spettro della matrice e
che genera una successione di matrici che trasformano per
similitudine la matrice data per ottenere una matrice triangolare
superiore. Dato il suo costo molto elevato e la complessità
dell'algoritmo non ce ne occuperemo, preferendo orientarci verso
un problema simile.
Ci concentriamo infatti su un metodo per ottenere quello che è
detto l'autovalore dominante, cioè l'autovalore di modulo massimo.
Anche se non risolviamo il problema originario, e quindi non
troviamo tutti gli autovalori della matrice ![]() , la soluzione a
questo problema è di grande interesse in molti problemi di
applicazione reale, ad esempio per la geosismica, per lo studio
delle vibrazioni di macchine e strutture ed addirittura in
meccanica quantistica.
, la soluzione a
questo problema è di grande interesse in molti problemi di
applicazione reale, ad esempio per la geosismica, per lo studio
delle vibrazioni di macchine e strutture ed addirittura in
meccanica quantistica.