Condizionamento delle operazioni fondamentali

Vogliamo adesso guardare come sono influenzate le operazioni fondamentali dell'aritmetica se applicate a dati perturbati, per fare questo abbiamo bisogno di alcune ipotesi preliminari: siano $x,y \in \mathbb{R}$ e siano $\hat{x}=x(1+\varepsilon x)$, $\hat{y}=y(1+\varepsilon y)$ i valori perturbati ed inoltre sia $\varepsilon = max \{ \vert\varepsilon x\vert, \vert\varepsilon y\vert \}$.

1. La somma e la sottrazione.
   
   $$z=x+y \quad \hat{z}=\hat{x}+\hat{y}=x(1+\varepsilon x)+y(1+\varepsilon y)$$
   
   
   
   
   $$\hat{z}=\underbrace{x+y}_{z} + x\varepsilon x + y\varepsilon y$$
   
   
   
   
   $$\vert\hat{z} - z\vert=\vert x\varepsilon x + y\varepsilon y\vert$$
   
   
   per la disuguaglianza triangolare
   
   $$\vert\hat{z} - z\vert \leq \vert x\vert\vert\varepsilon x\vert + \vert y\vert\vert\varepsilon y\vert$$
   
   
   
   
   $$\vert\hat{z} - z\vert \leq (\vert x\vert + \vert y\vert)\varepsilon$$
   
   
   possiamo allora porre
   
   $$\vert\varepsilon z\vert= \frac{\vert\hat{z}-z\vert}{\vert z\v... ... \frac{\vert x\vert + \vert y\vert}{\vert x+y\vert} \varepsilon$$
   
   
   per la somma abbiamo quindi un valore del numero di condizionamento pari a:
   
   $$k=\frac{\vert x\vert + \vert y\vert}{\vert x+y\vert}$$
   
   
   perciò il problema risulta mal condizionato quanto $\vert x+y\vert \approx 0$. Tutto quanto è stato detto per la somma vale in modo equivalente per la sottrazione, infatti non abbiamo posto alcun vincolo sul segno dei numeri $x,y$, perciò $x-y \equiv x+(-y)$.
   
2. Il prodotto.
   
   $$z=xy \quad \hat{z}=\hat{x} \hat{y}=x(1+\varepsilon x) y(1+\varepsilon y)$$
   
   
   
   
   $$\hat{z}=\underbrace{xy}_{z}(1+\varepsilon x + \varepsilon y ... ...lon x\varepsilon y) \approx z(1+\varepsilon x + \varepsilon y)$$
   
   
   
   
   $$\hat{z}=z+z(\varepsilon x + \varepsilon y)$$
   
   
   
   
   $$\vert\hat{z}-z\vert=\vert z\vert\vert\varepsilon x + \varepsi... ...vert z\vert(\vert\varepsilon x\vert + \vert\varepsilon y\vert)$$
   
   
   e nuovamente possiamo ottenere
   
   $$\vert\varepsilon z\vert= \frac{\vert\hat{z}-z\vert}{\vert z\vert} \leq 2\varepsilon$$
   
   
   risulta perciò un problema sempre ben condizionato.
   
3. La divisione.
   
   $$z=\frac{x}{y} \quad \hat{z}=\frac{\hat{x}}{\hat{y}}=\frac{x(... ...c{x}{y}}_{z} \cdot \frac{(1+\varepsilon x)}{(1+\varepsilon y)}$$
   
   
   ricordandosi adesso che la somma della serie geometrica è
   
   $$\frac{1}{1+\varepsilon y} \approx 1-\varepsilon y (+{\varepsilon y}^2 - \cdots)$$
   
   
   si ottiene
   
   $$\hat{z} \approx z(1+\varepsilon x)(1-\varepsilon y)$$
   
   
   
   
   $$\vert\varepsilon z\vert= \frac{\vert\hat{z}-z\vert}{\vert z\v... ...- \vert\varepsilon y\vert\mbox{ }\right\vert \leq 2\varepsilon$$
   
   
   e risulta ancora un problema sempre ben condizionato.

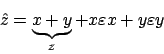
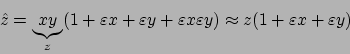
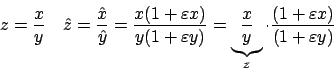
Quello che risulta conveniente fare è prima compiere le operazioni mal condizionate, per eseguire successivamente quelle ben condizionate; infatti, guardiamo il risultato di questo semplice esempio per vedere come questo può avere ripercussioni notevoli: siano $a=0.23371258 \times {10}^{-4}$, $b=0.33678429 \times {10}^2$ e $c=-0.3367781 \times {10}^{2}$ tre numeri di un sistema floating point con $\beta=10$ e $t=8$ proviamo allora sommare tra loro questi numeri:

$$\begin{eqnarray*} (a \oplus b) \oplus c & = & 0.33678452 \times 10^2 \ominus 0... ...lus 0.618000000 \times {10}^{-3} = 0.64137126 \times {10}^{-3} \end{eqnarray*}$$

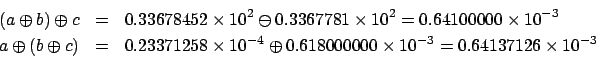
il risultato esatto è dato da: $a+b+c=0.641371258 \times {10}^{-3}$