Next: Sperimentazioni dell'algoritmo Up: Fattorizzazione Previous: Implementazione in Matlab Indice
La riga ![]() divide gli elementi sottodiagonali per
divide gli elementi sottodiagonali per
![]() , mentre la riga
, mentre la riga ![]() necessita di maggiori
chiarimenti. Tale riga modifica gli elementi che si trovano sotto
la riga i-esima e a destra della colonna i-esima escluse; vediamo
cosa succede nel caso
necessita di maggiori
chiarimenti. Tale riga modifica gli elementi che si trovano sotto
la riga i-esima e a destra della colonna i-esima escluse; vediamo
cosa succede nel caso 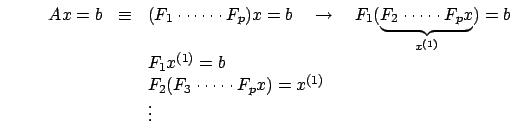 : moltiplichiamo
: moltiplichiamo ![]() ad
ad
![]()
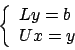
Concentriamoci adesso su ![]() : la matrice che otteniamo dal
prodotto ha la prima riga composta di elementi uguali a zero (la
prima componente di
: la matrice che otteniamo dal
prodotto ha la prima riga composta di elementi uguali a zero (la
prima componente di 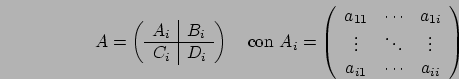 è nulla) e quindi possiamo considerare
è nulla) e quindi possiamo considerare
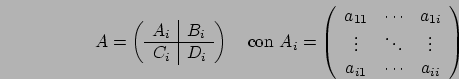 dal primo elemento non nullo in poi; inoltre la prima
colonna di
dal primo elemento non nullo in poi; inoltre la prima
colonna di ![]() risulta essere uguale ad
risulta essere uguale ad 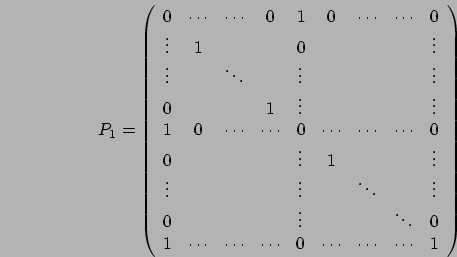 dal secondo
elemento in poi (il primo è zero): se la matrice così fatta fosse
sottratta direttamente ad
dal secondo
elemento in poi (il primo è zero): se la matrice così fatta fosse
sottratta direttamente ad ![]() teoricamente andrebbe ad
azzerare gli elementi sottodiagonali della prima colonna, ma
proprio in quelle posizioni abbiamo memorizzato gli elementi non
nulli del vettore
teoricamente andrebbe ad
azzerare gli elementi sottodiagonali della prima colonna, ma
proprio in quelle posizioni abbiamo memorizzato gli elementi non
nulli del vettore 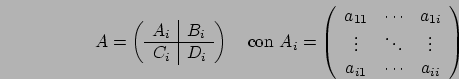 che quindi verrebbero modificati; possiamo
allora limitarci alla porzione suddetta.
che quindi verrebbero modificati; possiamo
allora limitarci alla porzione suddetta.
Passiamo adesso al costo computazionale: durante il passo i-esimo vengono eseguite:
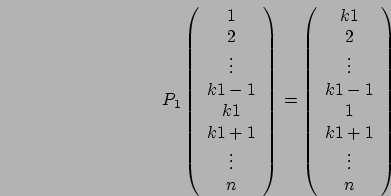 moltiplicazioni ed altrettante sottrazioni per
la riga
moltiplicazioni ed altrettante sottrazioni per
la riga
La fattorizzazione ha un costo proporzionale al cubo della
dimensione significativa; per risolvere il sistema lineare
associato ci sarà anche un costo proporzionale ad ![]() .
.
Morpheus 2004-01-04