Next: Gauss ci da una Up: Fattorizzazioni di matrici Previous: Fattorizzazioni di matrici Indice
La somma ed il prodotto di matrici triangolari, inferiori o superiori, sono ancora triangolari, inferiori o superiori; in particolare per gli elementi diagonali abbiamo
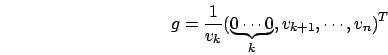
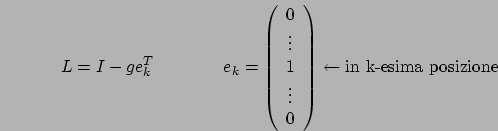
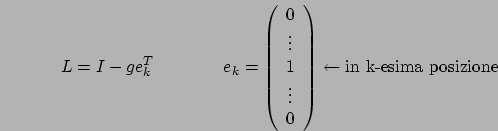
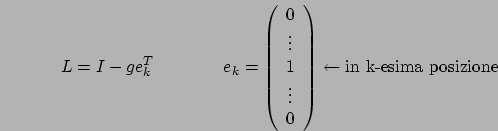
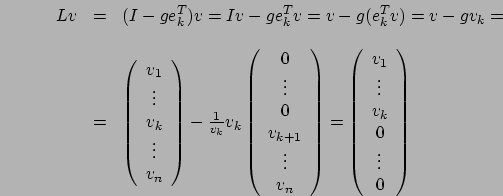 (A non
singolare)
(A non
singolare)
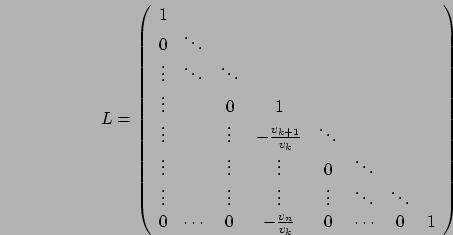
Consideriamo adesso un particolare caso di matrice triangolare, quella triangolare inferiore a diagonale unitaria
In questo caso il determinante di ![]() è sicuramente diverso da
zero, ed inoltre abbiamo che tutti gli autovalori della matrice
sono uguali ad uno:
è sicuramente diverso da
zero, ed inoltre abbiamo che tutti gli autovalori della matrice
sono uguali ad uno:
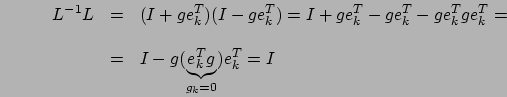 .
Dalle proprietà (2) e (3) si possono derivare queste due proprietà
delle matrici triangolari a diagonale unitaria:
.
Dalle proprietà (2) e (3) si possono derivare queste due proprietà
delle matrici triangolari a diagonale unitaria:
Se possiamo scrivere ![]() con
con