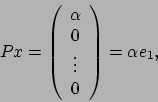Vediamo adesso il costo di questo algoritmo, analizzando le righe
significative per la complessità:
 viene eseguito un prodotto scalare di dimensione
viene eseguito un prodotto scalare di dimensione
 , quindi
, quindi 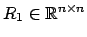 flops;
flops;
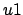 si esegue una somma ed un prodotto scalare di
dimensione
si esegue una somma ed un prodotto scalare di
dimensione  , quindi ancora
, quindi ancora 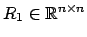 flops;
flops;
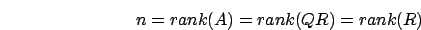 vi sono una somma ed una divisione, due operazioni
trascurabili, ma viene anche eseguito un prodotto matrice-vettore
di dimensioni
vi sono una somma ed una divisione, due operazioni
trascurabili, ma viene anche eseguito un prodotto matrice-vettore
di dimensioni
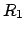 , quindi
, quindi 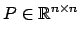 .
.
Sommando il costo del prodotto matrice-vettore (che è predominante
sul costo dei prodotti scalari) su 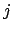 si perviene a:
si perviene a:
un costo proporzionale al cubo della dimensione significativa, un
costo sicuramente importante ma la metà di quello necessario alla
fattorizzazione 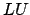 : il fatto di avere una matrice simmetrica ci
consente di ridurre di un fattore
: il fatto di avere una matrice simmetrica ci
consente di ridurre di un fattore 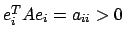 il costo della
fattorizzazione.
il costo della
fattorizzazione.
Morpheus
2004-01-04
![]() si perviene a:
si perviene a: