Next: Costo computazionale Up: Fattorizzazione Previous: Implementazione in Matlab Indice
Cerchiamo adesso di dare una spiegazione del codice appena visto.
Come si vede dall'introduzione teorica, durante il passo j-esimo
sia per il calcolo di ![]() che degli
che degli 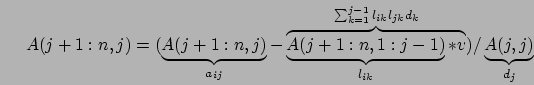
![]() viene
utilizzata la quantità
viene
utilizzata la quantità ![]() all'interno di una sommatoria
per
all'interno di una sommatoria
per
![]() ; risulta perciò utile memorizzare questi
valori in una forma comoda per il calcolo della sommatoria, e
questa forma ci viene fornita dall'algebra lineare: se si
memorizzasse, per esempio per il calcolo di
; risulta perciò utile memorizzare questi
valori in una forma comoda per il calcolo della sommatoria, e
questa forma ci viene fornita dall'algebra lineare: se si
memorizzasse, per esempio per il calcolo di ![]() , gli elementi
, gli elementi
![]() in un vettore riga e il fattore
in un vettore riga e il fattore ![]() in un vettore
colonna (chiamato da qui in avanti
in un vettore
colonna (chiamato da qui in avanti ![]() ), e se ne facesse il
prodotto scalare quello che si otterrebbe sarebbe proprio la
sommatoria da sottrarre ad
), e se ne facesse il
prodotto scalare quello che si otterrebbe sarebbe proprio la
sommatoria da sottrarre ad 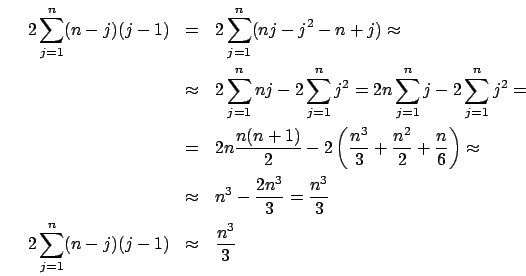 :
:
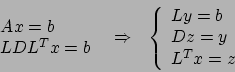
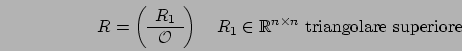 sono la diagonale della
matrice
sono la diagonale della
matrice
Per il calcolo della j-esima colonna di ![]() seguiamo le
indicazioni che ci vengono della teoria che tradotte in codice
portano alla riga
seguiamo le
indicazioni che ci vengono della teoria che tradotte in codice
portano alla riga ![]() :
: