Come si vede nel codice sopra abbiamo introdotto la quantità
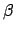 per un fatto di efficienza: infatti quello che vogliamo
rappresentare è
per un fatto di efficienza: infatti quello che vogliamo
rappresentare è
che sappiamo essere uno scalare. Tramite alcuni passi algebrici si
giunge al risultato che
e l'aver introdotto questo
fattore ci consente di spezzare il calcolo del prodotto tra la
matrice di Householder e la matrice 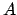 in modo da ridurre la
complessità: infatti calcolando esplicitamente
in modo da ridurre la
complessità: infatti calcolando esplicitamente 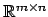 avremmo
ottenuto una matrice, che moltiplicata per
avremmo
ottenuto una matrice, che moltiplicata per 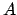 avrebbe aumentato
considerevolmente la complessità dell'algoritmo; in questo modo
riusciamo a calcolarci
avrebbe aumentato
considerevolmente la complessità dell'algoritmo; in questo modo
riusciamo a calcolarci  e successivamente
e successivamente  che è un
vettore e quindi vanno a moltiplicarsi due vettori, un costo
decisamente minore del prodotto matrice-matrice.
che è un
vettore e quindi vanno a moltiplicarsi due vettori, un costo
decisamente minore del prodotto matrice-matrice.
Per quanto riguarda il costo computazionale dividiamo il calcolo
per le righe significative:
- (1) si calcola una norma su un vettore di lunghezza
 che prevede il quadrato di ogni componente, la loro somma ed
infine estrarne la radice quadrata: un totale di
che prevede il quadrato di ogni componente, la loro somma ed
infine estrarne la radice quadrata: un totale di 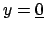 flops;
flops;
- (2) si eseguono
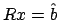 divisioni;
divisioni;
- (3) la parte più corposa dell'algoritmo si trova qua dentro,
infatti vengono eseguite circa
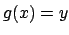 flops, metà per il
calcolo di
flops, metà per il
calcolo di  e le altre per l'aggiornamento della matrice.
e le altre per l'aggiornamento della matrice.
Allora, sommando su 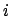 il costo della riga
il costo della riga 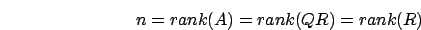 si ottiene
si ottiene
che nel caso quadrato 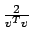 diventa un
costo proporzionale a
diventa un
costo proporzionale a
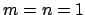 , non proprio l'ideale per
risolvere sistemi lineari.
, non proprio l'ideale per
risolvere sistemi lineari.
Morpheus
2004-01-04
![]() per un fatto di efficienza: infatti quello che vogliamo
rappresentare è
per un fatto di efficienza: infatti quello che vogliamo
rappresentare è
 che prevede il quadrato di ogni componente, la loro somma ed
infine estrarne la radice quadrata: un totale di
che prevede il quadrato di ogni componente, la loro somma ed
infine estrarne la radice quadrata: un totale di ![]() il costo della riga
il costo della riga ![]() si ottiene
si ottiene