Next: Implementazione in Matlab Up: Fattorizzazioni di matrici Previous: Sperimentazioni dell'algoritmo Indice
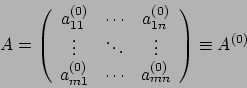
Quello che facciamo adesso è cercare una fattorizzazione di ![]() come un fattore ortogonale ed un fattore triangolare superiore.
come un fattore ortogonale ed un fattore triangolare superiore.
Data
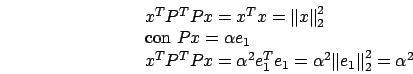 (in
generale ha più righe che colonne) e richiediamo che abbia rango
massimo, cioè
(in
generale ha più righe che colonne) e richiediamo che abbia rango
massimo, cioè ![]() (e quindi se la matrice è quadrata, sarà
anche non singolare). Allora ciò che cerchiamo è
(e quindi se la matrice è quadrata, sarà
anche non singolare). Allora ciò che cerchiamo è
Mostreremo l'esistenza di questa fattorizzazione mediante una dimostrazione costruttiva che ci guiderà nella costruzione dell'algoritmo.
Dalle proprietà del rango abbiamo che
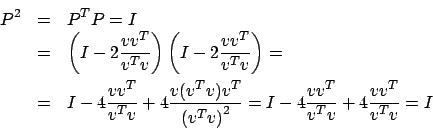
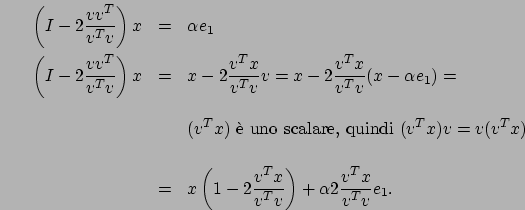 è non singolare.
è non singolare.
Dunque, come già visto durante l'algoritmo di eliminazione di
Gauss, dato un vettore ![]() cerchiamo una matrice ortogonale
cerchiamo una matrice ortogonale
![]() tale che:
tale che:
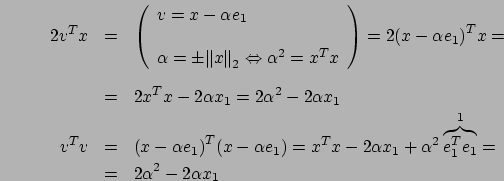 si ottiene:
si ottiene:
Cerchiamo dunque una matrice 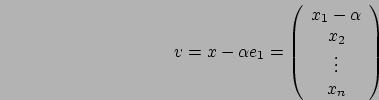 nella forma
nella forma
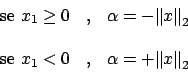
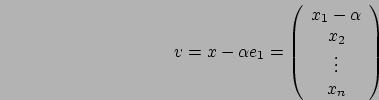 è una matrice simmetrica,
perché sia
è una matrice simmetrica,
perché sia 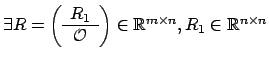 verifichiamo l'ortogonalità di P:
verifichiamo l'ortogonalità di P:
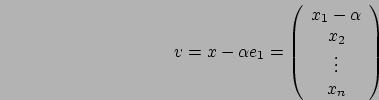 è ottenuta come
la matrice identità a cui viene sommata una matrice di correzione
di rango
è ottenuta come
la matrice identità a cui viene sommata una matrice di correzione
di rango
Eravamo rimasti che il vettore ![]() doveva essere determinato,
verifichiamo allora che
doveva essere determinato,
verifichiamo allora che
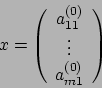
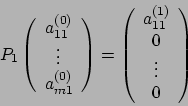

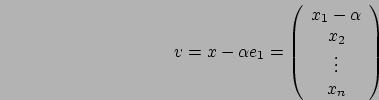 così costruita soddisfa le nostre richieste; il
vettore
così costruita soddisfa le nostre richieste; il
vettore
La scelta del segno di ![]() , cioè se scegliere
, cioè se scegliere
![]() oppure
oppure
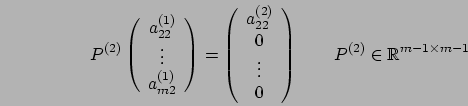 , è sottesa alla riduzione
degli errori nell'aritmetica finita del calcolatore (la matrice
ortogonale non pone grossi problemi di calcolo poichè
l'imposizione che la somma dei quadrati sia pari ad uno la rende
tale che gli elementi siano ben limitati in modulo e quindi che
anche gli errori sono limitati). Come detto
, è sottesa alla riduzione
degli errori nell'aritmetica finita del calcolatore (la matrice
ortogonale non pone grossi problemi di calcolo poichè
l'imposizione che la somma dei quadrati sia pari ad uno la rende
tale che gli elementi siano ben limitati in modulo e quindi che
anche gli errori sono limitati). Come detto
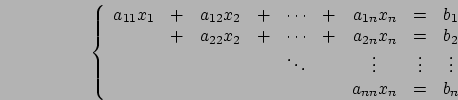 ed
ed  fosse l'elemento di modulo massimo), dunque
fosse l'elemento di modulo massimo), dunque
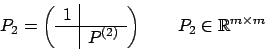

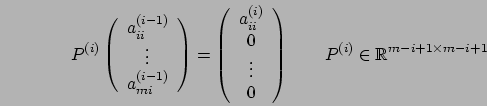 ortogonale ed
ortogonale ed
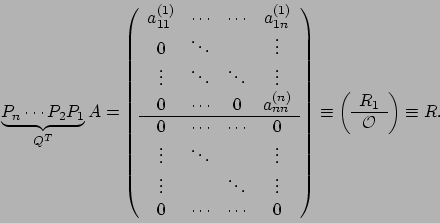
La dimostrazione di questo teorema definirà un algoritmo che ci
consentirà di generare la fattorizzazione. Ragioniamo come abbiamo
fatto con l'eliminazione di Gauss: quindi poniamo
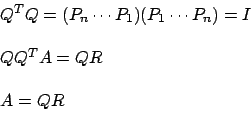
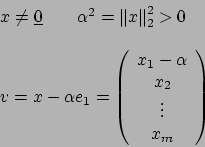
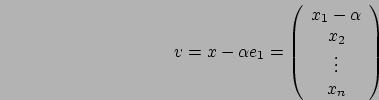 sarà sempre ben
definita.
sarà sempre ben
definita.
Ottenuta la matrice ![]() possiamo operare come già esaminato con
Gauss
possiamo operare come già esaminato con
Gauss
Consideriamo la seconda colonna, dall'elemento diagonale in poi e
definiamo la matrice 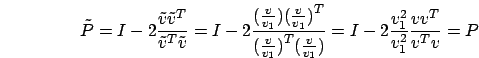 in modo tale che
in modo tale che
In generale, al passo i-esimo
Nel caso di matrici quadrate, se la matrice in esame è non
singolare, allora è anche fattorizzabile  , mentre per la
fattorizzazione
, mentre per la
fattorizzazione ![]() , come ci ricordiamo, ci sono ben altri
vincoli, molto più stringenti che la semplice non singolarità.
, come ci ricordiamo, ci sono ben altri
vincoli, molto più stringenti che la semplice non singolarità.
Soffermiamoci sullo spazio di memoria di cui abbiamo bisogno. Ci
riferiremo al primo passo, dal momento che gli altri sono simili.
Per conoscere ![]() l'unica cosa di cui abbiamo bisogno è il
vettore
l'unica cosa di cui abbiamo bisogno è il
vettore ![]() , che ha dimensioni
, che ha dimensioni ![]() : infatti noto
: infatti noto ![]() , possiamo
ricavare
, possiamo
ricavare ![]() .
.
Dato che ![]() è massimo
è massimo
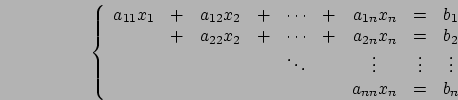 ed
ed 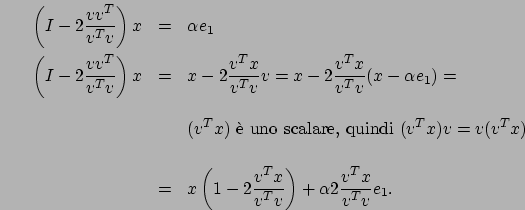 mentre nelle parti che
andiamo ad azzerare metteremo i vettori
mentre nelle parti che
andiamo ad azzerare metteremo i vettori