Il Value-Passing

Finora abbiamo parlato di azioni ed operatori ai quali non è associato alcun valore. Ci siamo infatti riferiti al calcolo di base per modellare sistemi concorrenti. Esiste però la possibilità di utilizzare calcoli con Value-Passing nei quali, oltre alla pura sincronizzazione, si esprime la comunicazione di valori di qualsiasi tipo; infatti questo tipo di calcolo tramite opportuni accorgimenti può essere ricondotto al calcolo base.

Per semplificare lo studio, assumiamo che tutti i valori appartengono ad un fissato insieme V che può contenere qualunque tipo di elementi. L'esempio più immediato che si può fare è il seguente:

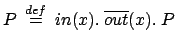$$P \: \stackrel{{def}}{{=}}\: in(x).\:\overline{out}(x).\:P$$   tale che$$\quad x \in V$$

Con questa definizione, il processo P può ricevere in input (porta $in$) uno qualsiasi dei valori in V e subito dopo spedirlo come output (dalla porta $out$).

Le derivazioni di questo sistema saranno le seguenti:

$$P \: \stackrel{in(v)}{\longrightarrow} \: \overline{out}(v).\:P \: \stackrel{\overline{out}(v)}{\longrightarrow} \: P \quad$$

dove $v$ è l'elemento dell'insieme V che passa nel sistema.

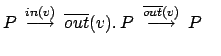
Se l'insieme V è finito, allora si può tradurre qualunque processo in uno descritto con il calcolo senza Value-Passing. Nell'esempio sopra basta dare la possibilità a P di scegliere uno qualunque degli elementi di V da prendere in input e questo si fa utilizzando la seguente sommatoria:

$$P \: \stackrel{{def}}{{=}}\: \sum_{v \in V} in_v.\:\overline{out_v}.\:C$$

dove $\:in_v\:$ e $\overline{out_v}$ sono rispettivamente le azioni di input e output relative ai diversi $\:v \in$V (al variare di $v \in$V).

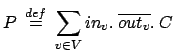
Nel caso visto sopra la variabile è associata ad un'azione visibile ($\tau$ non può riferirsi a nessun valore), ma essa può anche essere collegata ad un processo. La forma generica 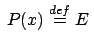$\:P(x) \stackrel{{def}}{{=}}E \:$ può essere tradotta nel seguente insieme di definizioni del calcolo di base:

$$\{P_v \: \stackrel{{def}}{{=}}\: E[v/x]$$   t.c.$$\quad v \in V \}$$

dove i vari $P_v$ sono nuovi nomi di processi in cui al posto della variabile si inserisce uno dei valori del dominio.

Altri operatori che subiscono modifiche in questa traduzione sono la restrizione e il relabelling. Nel primo caso l'insieme di restrizione L diventa $\:\{\alpha_v : \alpha \in L, v\in$V$\}\:$; la funzione di relabelling f è modificata in modo che $\:\hat{f}(\alpha_v) = f(\alpha)_v \:$.

Esempio 2..1   Con il Value-Passing si può definire il seguente conto alla rovescia in modo veloce:

$(x = 3)$
COUNTDOWN(x)	$\:\stackrel{{def}}{{=}}\:$	$tick$.COUNTDOWN(x-1) $\quad$ con $\quad x \not=0$
COUNTDOWN(0)	$\:\stackrel{{def}}{{=}}\:$	$beep.\:nil$

Senza Value-Passing si ottiene una descrizione più lunga ma con le stesse informazioni:

COUNTDOWN$_3$	$\:\stackrel{{def}}{{=}}\:$	$tick$. COUNTDOWN$_2$
COUNTDOWN$_2$	$\:\stackrel{{def}}{{=}}\:$	$tick$. COUNTDOWN$_1$
COUNTDOWN$_1$	$\:\stackrel{{def}}{{=}}\:$	$tick$. COUNTDOWN$_0$
COUNTDOWN$_0$	$\:\stackrel{{def}}{{=}}\:$	$beep.\:nil$