Next: Equivalenze di bisimulazione Up: Equivalenze fra processi Previous: Equivalenza per fallimenti Indice
Un'elegante caratterizzazione alternativa della failure equivalence è chiamata testing equivalence, secondo la quale due processi sono equivalenti quando passano gli stessi test.
Consideriamo dunque un processo P definito su
![]() ed un
osservatore O definito su
ed un
osservatore O definito su
![]() dove
dove
![]() è l'azione che indica il soddisfacimento dell'osservatore.
Un'osservatore può essere visto come un agente che svolge dei test
specifici sui processi. Il risultato del test di O su P viene
indicato con una computazione
è l'azione che indica il soddisfacimento dell'osservatore.
Un'osservatore può essere visto come un agente che svolge dei test
specifici sui processi. Il risultato del test di O su P viene
indicato con una computazione
![]() , l'insieme
non vuoto di tutte le computazioni possibili. Naturalmente ora
dobbiamo definire cos'è una computazione:
, l'insieme
non vuoto di tutte le computazioni possibili. Naturalmente ora
dobbiamo definire cos'è una computazione:
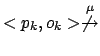 per ogni
per ogni
Si ha quindi:
Il significato di quanto scritto sopra è che nel caso may deve esistere almeno una computazione in cui due processi eseguono la stessa sequenza di azioni ed alla fine il processo osservatore è soddisfatto; nel caso must, qualsiasi computazione deve portare al soddisfacimento dell'osservatore.
Con le definizioni appena riportate si possono introdurre i
preordini (indichiamo con
![]() l'insieme degli
osservatori):
l'insieme degli
osservatori):
Come detto, prendendo in considerazione i kernel di questi due preordini possiamo definire la may-equivalence e la must-equivalence rispettivamente in questo modo:
Infine possiamo definire il preordine di testing e l'equivalenza di testing (o testing equivalence) tra due processi come:
La testing equivalence uguaglia tutti i processi che possono superare gli stessi test, ovvero soddisfare gli stessi osservatori, mentre nell'equivalenza per fallimenti avevamo che i processi venivano uguagliati in base ai test che non venivano superati. Come già detto all'inizio, queste due equivalenze sono identiche in CCS.
Morpheus 2004-02-10