Next: Simulazione e doppia simulazione Up: Equivalenze di bisimulazione Previous: Bisimulazione ed equivalenza forte Indice
Abbiamo appena visto la nozione di bisimulazione forte, nella
quale ogni azione ![]() di un processo deve corrispondere ad
un'azione
di un processo deve corrispondere ad
un'azione ![]() dell'altro, anche per le azioni
dell'altro, anche per le azioni ![]() . Quanto
faremo adesso sarà rilassare questa richiesta ed ottenendo dunque
una relazione più debole (in quanto identifica più processi): ciò
che si richiede ora è che ogni azione
. Quanto
faremo adesso sarà rilassare questa richiesta ed ottenendo dunque
una relazione più debole (in quanto identifica più processi): ciò
che si richiede ora è che ogni azione ![]() venga corrisposta con
zero o più azioni
venga corrisposta con
zero o più azioni ![]() . Questo ci porterà alla definizione di
bisimulazione debole e quindi alla definizione di una
equivalenza debole o, come viene più spesso chiamata,
dell'equivalenza osservazionale.
. Questo ci porterà alla definizione di
bisimulazione debole e quindi alla definizione di una
equivalenza debole o, come viene più spesso chiamata,
dell'equivalenza osservazionale.
Procederemo in modo analogo a quanto fatto per l'equivalenza forte, rimandando al capitolo relativo alla bisimulazione la visione di una serie di importanti risultati.
Cerchiamo dunque una nozione di equivalenza, che chiameremo equivalenza osservazionale, che rispetti la seguente proprietà:
p e q sono osservazionalmente equivalenti sse, per ogni azione, ogni derivazione da p tramite
è osservazionalmente equivalente a qualche discendenza da q tramite l'azione
, e similmente per il viceversa.
Chiameremo questa equivalenza ![]() e formalmente scriviamo:
e formalmente scriviamo:
pq sse,
(
)
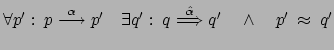 ;
;
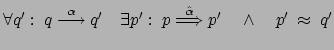 .
.
dove
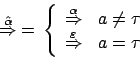
Operando in modo analogo a quanto fatto per la strong
bisimulation, cerchiamo ora la più grande relazione che soddisfi
(
![]() ); procediamo dunque come già visto:
); procediamo dunque come già visto:
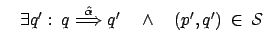
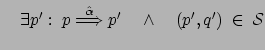
Possiamo ora definire l'equivalenza osservazionale, o bisimilarità:
Morpheus 2004-02-10