Next: Il metodo di Newton Up: Metodo di Newton Previous: Implementazione in Matlab (radici Indice
Eseguiamo l'algoritmo sulla stessa funzione del metodo di bisezione e guardiamo il risultato:
» [x,it,tolf]=newton(0,'fxcosx','dfxcosx',1e-15,2000)
x =
0.73908513321516
it =
5
tolf =
1.673612029183215e-015
»
impiega circa un decimo delle iterazioni di bisezione. Si deve comunque tenere presente che ad ogni iterazione si devono valutare due funzioni, e da non trascurare è il costo del calcolo analitico della derivata della funzione.
Proviamo adesso ad applicare l'algoritmo a due funzioni a radici
multiple, per mostrare quanto lentamente converge verso la
soluzione; la prima funzione che vedremo è
![]() che
ammette come soluzione
che
ammette come soluzione ![]() :
:
» [x,it,tolf]=newton(0,'fx5','dfx5',1e-15,2000)
x =
4.99999999999999
it =
155
tolf =
7.470729841072302e-072
»
impiega ben ![]() iterazioni per raggiungere un'approssimazione
neanche troppo precisa della soluzione: vedremo come si riuscirà
ad ottenere risultati molto migliori (perfino il metodo di
bisezione ottiene risultati migliori, impiegando soltanto
iterazioni per raggiungere un'approssimazione
neanche troppo precisa della soluzione: vedremo come si riuscirà
ad ottenere risultati molto migliori (perfino il metodo di
bisezione ottiene risultati migliori, impiegando soltanto ![]() iterazioni).
iterazioni).
La seconda funzione che andremo a vedere è leggermente più
complessa ed è
![]() e otteniamo come risultato
e otteniamo come risultato
» [x,it,tolf]=newton(0,'fxm','dfxm',1e-15,2000)
x =
1.00000000000000
it =
117
tolf =
2.772655121618958e-058
»
certamente un risultato non esaltante per un metodo così oneroso come Newton.
Quello che abbiamo intenzione di mostrare adesso è come la scelta
del punto iniziale possa influenzare la convergenza del metodo
verso una soluzione oppure verso un'altra; la funzione che
prenderemo in esame è la semplice 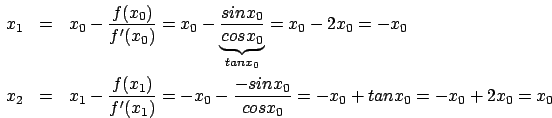 e cambiando punto
di partenza otteniamo due delle sue infinite soluzioni:
e cambiando punto
di partenza otteniamo due delle sue infinite soluzioni:
» [x,it,tolf]=newton(1,'sin','cos',1e-15,2000)
x =
0
it =
5
tolf =
1.000000000000000e-015
» [x,it,tolf]=newton(2,'sin','cos',1e-15,2000)
x =
3.14159265358979
it =
6
tolf =
1.000000000000000e-015
»
in un caso abbiamo scelto ![]() ed il metodo converge verso la
soluzione
ed il metodo converge verso la
soluzione
![]() , nel secondo caso, invece, si è scelto
, nel secondo caso, invece, si è scelto
![]() e la successione di approssimazioni converge verso la
soluzione
e la successione di approssimazioni converge verso la
soluzione
![]()
Come la scelta del punto iniziale può portare a convergere verso
una soluzione piuttosto che verso un'altra (nel caso ce ne siano
più d'una), questa può anche portare a non convergere il metodo di
Newton come vedremo adesso. Consideriamo la funzione ![]() che è continua e derivabile su tutto
che è continua e derivabile su tutto ![]() . Cerchiamo il
punto iniziale tale che
. Cerchiamo il
punto iniziale tale che
» type fnonew
function y=fnonew(x);
y=atan(abs(x))-2*abs(x).*dfatanx(x);
» x0=bisezione(0.1,3,'fnonew',1e-15)
x0 =
1.39174520027073
» fnonew(x0)
ans =
1.110223024625157e-016
»
![]() è il punto che stavamo cercando; ci si presentano due scelte:
porre
è il punto che stavamo cercando; ci si presentano due scelte:
porre ![]() oppure
oppure ![]() entrambe interessanti, vediamo
perché:
entrambe interessanti, vediamo
perché:
» [x,it]=newton(x0,'fatanx','dfatanx',1e-10,2000)
x =
1.39174520027073
x =
-1.39174520027073
x =
1.39174520027073
......
it =
2000
»
» newton(3,'fatanx','dfatanx',1e-10,2000)
x1 =
-9.49045772398254
x1 =
1.239995111788842e+002
.............
x1 =
1.554292211858608e+146
x1 =
-3.794767904961391e+292
x1 =
Inf
Nel primo caso vediamo come la funzione continui ad alternarsi tra
![]() ed
ed ![]() senza mai convergere verso la soluzione; nel
secondo caso, invece, si vede come scegliendo un valore maggiore
di quell'
senza mai convergere verso la soluzione; nel
secondo caso, invece, si vede come scegliendo un valore maggiore
di quell'![]() la successione delle approssimazioni diverga verso
infinito. Scegliendo un valore appena inferiore ad
la successione delle approssimazioni diverga verso
infinito. Scegliendo un valore appena inferiore ad ![]() e
precisamente
e
precisamente 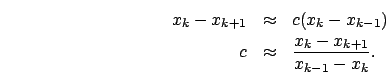 , dove con
, dove con ![]() indichiamo la precisione
di macchina, il metodo di Newton converge, come si vede
indichiamo la precisione
di macchina, il metodo di Newton converge, come si vede
» [x,it,tolf]=newton(x0-eps,'fatanx','dfatanx',1e-15,2000)
x =
-2.073113138404900e-019
it =
41
tolf =
1.000000000000000e-015
»
Vogliamo dare anche un esempio di come a volte le approssimazioni
possano creare non pochi problemi. Prendiamo nuovamente in esame
la funzione 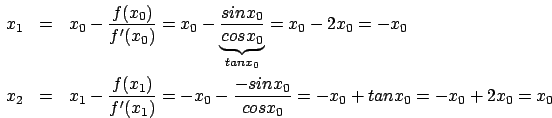 e cerchiamo come punto iniziale
e cerchiamo come punto iniziale
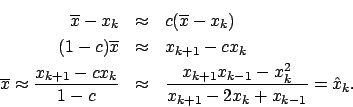
In due passi siamo tornati al punto di partenza. Calcoliamo il
punto iniziale ![]() ancora tramite il metodo di bisezione:
ancora tramite il metodo di bisezione:
» f
f =
Inline function:
f(x) = tan(x)-2*x
» x0=bisezione(1,pi/2-eps,f,1e-15s)
x0 =
1.16556118520721
» f(x0)
ans =
-4.440892098500626e-016
»
proviamo dunque ad applicare il metodo di Newton innescato con questo punto:
» [x,it,tolf]=newton(x0,'sin','cos',1e-15,2000)
x1 =
-1.16556118520721
x1 =
1.16556118520721
x1 =
-1.16556118520719
x1 =
1.16556118520712
...............
x =
0
it =
26
tolf =
1.000000000000000e-019
»
Al contrario di quanto ci si aspettava l'algoritmo converge! E questo è proprio dovuto alle approssimazioni fatte; se si guarda le prime due iterazioni, l'algoritmo si composta come previsto, ma già dalla terza inizia a perdere precisione sull'ultima cifra significativa, ed è questo fatto che porta alla convergenza il metodo.
Morpheus 2004-01-04