Next: Convergenza di Newton con Up: Soluzione di equazioni non Previous: Sperimentazioni dell'algoritmo Indice
Per questo metodo si richiede che
![]() che
significa che la funzione deve essere continua, derivabile e a
derivata continua ma non si suppone l'esistenza della soluzione
come si faceva nel metodo di bisezione.
che
significa che la funzione deve essere continua, derivabile e a
derivata continua ma non si suppone l'esistenza della soluzione
come si faceva nel metodo di bisezione.
Il metodo di Newton approssima la funzione con la retta tangente
ad essa nel punto di coordinate ![]() e si prende il
nuovo punto di approssimazione come l'intersezione di questa retta
con l'asse delle
e si prende il
nuovo punto di approssimazione come l'intersezione di questa retta
con l'asse delle ![]() , reiterando nuovamente il procedimento. Se
sviluppiamo nuovamente la funzione in serie di Taylor arrestandoci
al primo ordine si ottiene:
, reiterando nuovamente il procedimento. Se
sviluppiamo nuovamente la funzione in serie di Taylor arrestandoci
al primo ordine si ottiene:
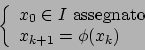
 quello che
si ottiene è
quello che
si ottiene è
La convergenza del metodo di Newton è locale, cioè si deve
scegliere ![]() abbastanza vicino ad
abbastanza vicino ad ![]() perché il
metodo converga; questo inconveniente non si aveva con il metodo
di bisezione, che garantiva la convergenza qualsiasi fosse
l'intervallo scelto (che rispettasse le richieste).
perché il
metodo converga; questo inconveniente non si aveva con il metodo
di bisezione, che garantiva la convergenza qualsiasi fosse
l'intervallo scelto (che rispettasse le richieste).
 ed un intorno di
ed un intorno di  tale che
tale che
![]()
Dividiamo adesso lo studio della convergenza nel caso di radici semplici e radici multiple, definendo prima cosa si intenda per molteplicità di una radice: