Next: Aritmetica floating point Up: Approssimazione Previous: Approssimazione Indice
Proviamo con un esempio a spiegare il funzionamento dei due
metodi: consideriamo
![]() ed
ed ![]() , sia
, sia
![]() ; naturalmente questo numero non può essere
rappresentato in modo esatto con un elemento dell'insieme
; naturalmente questo numero non può essere
rappresentato in modo esatto con un elemento dell'insieme
![]() (il numero di cifre significative è superiore al
nostro limite); vediamo come si comportano allora troncamento ed
arrotondamento:
(il numero di cifre significative è superiore al
nostro limite); vediamo come si comportano allora troncamento ed
arrotondamento:
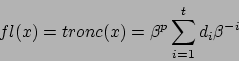

Il significato del ![]() è che, nel caso
è che, nel caso ![]() deve essere
utilizzato il ``
deve essere
utilizzato il ``![]() '', mentre per
'', mentre per ![]() si deve utilizzare
``
si deve utilizzare
``![]() ''.
''.
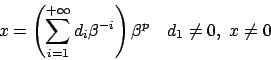
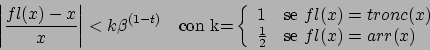
Il numero
![]() è detto precisione di macchina,
ed è il più piccolo numero positivo tale che:
è detto precisione di macchina,
ed è il più piccolo numero positivo tale che:
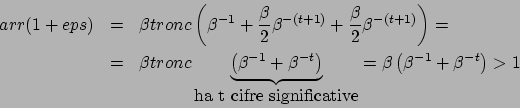
Per verificare
![]() scegliendo
scegliendo
![]() si otterrà, alla fine di una
sequenza di espressioni simili a quelle sopra, un qualcosa di
minore di
si otterrà, alla fine di una
sequenza di espressioni simili a quelle sopra, un qualcosa di
minore di ![]() che verrà scartato dall'operazione di
troncamento.
che verrà scartato dall'operazione di
troncamento.
Morpheus 2004-01-04