Aritmetica floating point

Sull'insieme dei numeri macchina si definisce l'aritmetica di macchina che differisce dall'aritmetica esatta, vediamo come:

$$\begin{array}{l} x \oplus y = fl(x+y) = (x+y)(1+\varepsilo... ...\ x \oslash y = fl(x/y) = (x/y)(1+\varepsilon) \end{array}$$

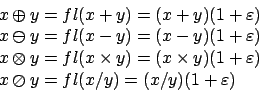
Quanto scritto sopra è derivato dal fatto che

$$\left\vert \frac{fl(x) - x}{x} \right\vert \leq eps$$

da cui si ricava che $fl(x)=x(1+ \varepsilon)$: infatti possiamo scrivere la precedente relazione come $\vert fl(x)-x\vert \leq \vert x\vert \cdot eps$ e da qui, prendendo $\vert\varepsilon\vert \leq eps$ si ottiene $\vert fl(x)-x\vert=\vert x\vert \vert\varepsilon\vert$.

Il significato della precedente scrittura è che la singola operazione macchina commette al più un errore dell'ordine di $eps$: se $x,y,x \in \mathbb{F}$

$$x \oplus y \oplus z \neq (x+y+z)(1+\varepsilon) \quad \vert\varepsilon\vert \leq eps$$