In questo caso si usano quelle che sono dette matrici di
compagnia, vediamo la loro struttura:
praticamente una matrice con tutti valori nulli tranne
la prima sottodiagonale e la prima riga, che contiene dei valori
generici.
Proposizione 1
Se 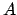 è una matrice di compagnia allora
è una matrice di compagnia allora
Facciamo un esempio: considerando la seguente matrice
calcoliamone adesso il polinomio caratteristico come il
determinante di 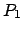 rispetto alla terza colonna:
rispetto alla terza colonna:
Detto questo possiamo costruire una matrice 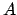 con
fissato: infatti dato di grado n, e cioè nella forma
con
fissato: infatti dato di grado n, e cioè nella forma
possiamo scrivere la matrice
Un paio di osservazioni sono d'obbligo:
- Con la matrice
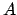 sopra definita, se avessimo
conosceremmo anche gli autovalori di B, infatti sia
e sia
sopra definita, se avessimo
conosceremmo anche gli autovalori di B, infatti sia
e sia  l'autovettore corrispondente allora
l'autovettore corrispondente allora
e quindi  e
autovettore anche di
e
autovettore anche di 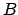 , oltre che di
, oltre che di 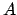 , e l'autovalore
corrispondente è .
, e l'autovalore
corrispondente è .
- Se avessimo allora
sia ancora
e
 l'autovettore
corrispondente allora
l'autovettore
corrispondente allora
facilmente verificabile
per induzione.
Morpheus
2004-01-04
![]() rispetto alla terza colonna:
rispetto alla terza colonna:
![]() con
fissato: infatti dato di grado n, e cioè nella forma
con
fissato: infatti dato di grado n, e cioè nella forma