A diagonale

Se la matrice è una matrice diagonale, allora assume la forma

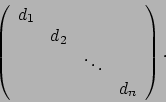
$\begin{displaymath}\left( \begin{array}{cccc} d_1 & & & \\ & d_2 & \\ & & \ddots &\\ & & & d_n \end{array} \right)\mbox{.} \end{displaymath}$

Il determinante di una matrice siffatta è dato dal prodotto degli elementi diagonali

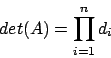
$\begin{displaymath}det(A)=\prod_{i=1}^n d_i\end{displaymath}$

e risulta diverso da zero se e solo se $\forall i=1,\cdots,n \mbox{ } d_i \neq 0$ .

La struttura a diagonale facilita molto il calcolo del vettore , perché equivale ad avere equazioni disaccoppiate, infatti

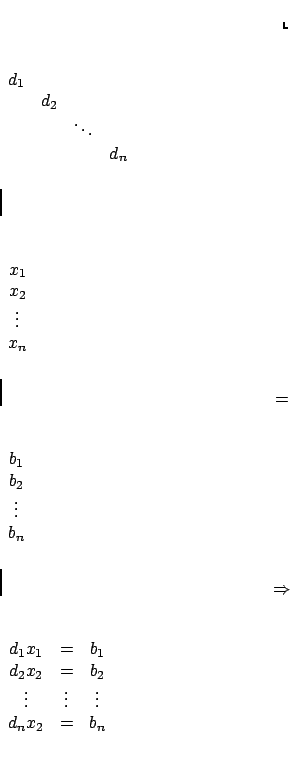
$\begin{displaymath} \begin{array}{cccccc} \end{displaymath}$

(
$\begin{array}{cccc} d_1 & & & \\ & d_2 & \\ & & \ddots &\\ & & & d_n \end{array}$
)

$\begin{displaymath}& \par \end{displaymath}$

(
$\begin{array}{c} x_1\\ x_2 \\ \vdots\\ x_n \end{array}$
)

$\begin{displaymath} & = & \end{displaymath}$

(
$\begin{array}{c} b_1\\ b_2 \\ \vdots\\ b_n \end{array}$
)

$\begin{displaymath} & \Rightarrow & \par \end{displaymath}$

{
$\begin{array}{ccc} d_1x_1 & = & b_1 \\ d_2x_2 & = & b_2 \\ \vdots & \vdots & \vdots \\ d_nx_2 & = & b_n \end{array}$
.

$\begin{displaymath} \end{array} \end{displaymath}$

e quindi ciascuna equazione specifica una componente della soluzione

$\begin{displaymath}x_i = \frac{b_i}{d_i} \qquad i=1,\cdots,n\end{displaymath}$

e sono tutte espressioni ben definite perché sappiamo che gli elementi diagonali sono tutti non nulli.

Invece di un problema di dimensione , abbiamo risolto problemi di dimensione , e quindi impieghiamo flops.

Anche l'occupazione di memoria risulta lineare: non è necessario utilizzare una matrice 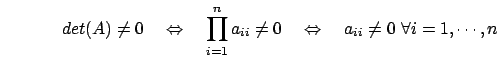$n\times n$ perché se sappiamo già che questa sarà diagonale ci basterà memorizzare gli elementi non nulli (quelli diagonali) in un vettore.

Morpheus 2004-01-04