Risoluzione di sistemi lineari

Il problema che andiamo ad affrontare adesso è quello di risolvere un sistema lineare, trovare cioè quei valori $x_1, \cdots, x_n$ tali da soddisfare il seguente sistema di equazioni:

$$\left\{ \begin{array}{ccccccccc} a_{11}x_1 & + & a_{12}x_2 ... ... & + & \cdots & + & a_{nn}x_n & = & b_n \end{array} \right.$$

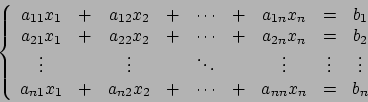
che scritto nel compatto e semplice linguaggio matematico significa trovare quel vettore reale $x$ tale che vaga l'uguaglianza:

$$Ax=b \qquad \qquad A \in \mathbb{R}^{n\times n}, \quad b,x \in \mathbb{R}^n\mbox{.}$$

L'ipotesi che faremo da qui in avanti sarà che $det(A) \neq 0$ cioè che la matrice $A$ sia non singolare. Formalmente, e sotto questa ipotesi, potremmo trovare il vettore $x$ come $x={A}^{-1}b$ ma questo comporta il calcolo dell'inversa di $A$ che risulta eccessivamente oneroso e per questo è una possibilità che non viene quasi mai utilizzata.

Dapprima vediamo casi semplici, in qui la soluzione del sistema lineare risulta quasi immediata grazie a forme particolari che $A$ può assumere, per poi passare nel caso generale.