A ortogonale

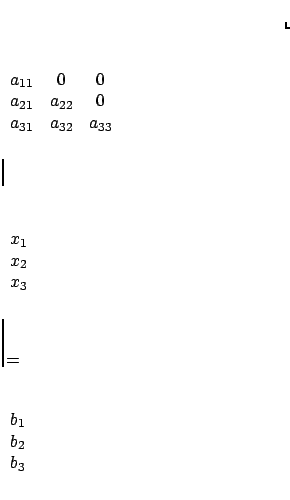Come sappiamo, se $A$ è una matrice ortogonale, allora rispetta la proprietà che $AA^T=I$ ed in questo caso abbiamo già la matrice inversa disponibile: basta moltiplicare a sinistra per $A^{-1}$ per ottenere la relazione $A^{-1}=A^T$. Questo è dunque un caso in cui il vettore $x$ è calcolato tramite la matrice inversa:

$$Ax=b \quad \rightarrow \quad x=A^{-1}b \equiv A^Tb$$

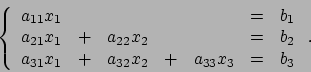
La soluzione la troviamo al costo di un prodotto matrice-vettore, che come sappiamo esegue $2n^2$ flops.

Naturalmente la scelta dell'algoritmo (i,j) oppure (j,i) risulta rilevante: per quanto detto prima dobbiamo optare per l'algoritmo che si adatta al nostro linguaggio di programmazione.