Next: Implementazione in Matlab Up: Risoluzione di sistemi lineari Previous: A ortogonale Indice
Se la matrice ![]() è triangolare inferiore si presenta nella forma
è triangolare inferiore si presenta nella forma
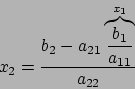
Proviamo con un esempio di una matrice triangolare inferiore ![]() a vedere come funziona il modo di risoluzione:
a vedere come funziona il modo di risoluzione:
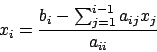
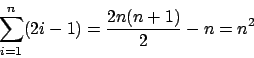

Si vede che la prima componente del vettore soluzione ![]() ,
, 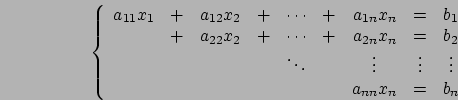 ,
è già disponibile, per cui possiamo trovare
,
è già disponibile, per cui possiamo trovare
Noto 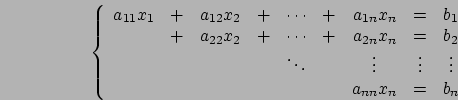 , possiamo adesso ricavare
, possiamo adesso ricavare ![]() nel seguente modo
nel seguente modo
Quello che abbiamo cercato di fare con questo semplice esempio era
mostrare come si poteva ottenere il vettore ![]() : tramite un
algoritmo iterativo si ottengono le componenti del vettore
soluzione tramite la relazione
: tramite un
algoritmo iterativo si ottengono le componenti del vettore
soluzione tramite la relazione
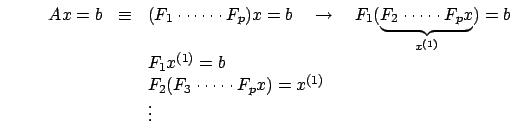 si arriva alla soluzione desiderata.
si arriva alla soluzione desiderata.