A matrice generica

Naturalmente non possiamo certo limitarci a risolvere sistemi lineari solo nei casi particolari appena visti: questi ci servivano come esempi di risoluzioni abbastanza semplici. Ma nel caso di $A$ generica come procediamo? Riuscendo a fattorizzare la matrice data in matrici di cui conosciamo la risoluzione del sistema lineare associato, e cioè se riusciamo a scrivere

$$A= F_1 \cdot F_2 \cdot F_3 \cdot \cdots \cdot F_p \qquad F_i... ... triangolare \\ diagonale \\ ortogonale \end{array} \right.$$

riuscendo a ridurre anche di molto l'ordine di grandezza del problema.

La non singolarità di $A$ ci porta a dire che

$$0 \neq det(A) = det(F_1 \cdot F_2 \cdot \cdots \cdot F_p) = \prod_{i=1}^p det(F_i) \Rightarrow det(F_i) \neq 0 \forall i$$

e dunque possiamo risolvere il sistema lineare $Ax=b$ come

$$\begin{array}{ccl} Ax=b & \equiv & (F_1 \cdot \cdot \cdots... ... \cdot \cdots \cdot F_px)=x^{(1)}\\ & & \vdots \end{array}$$

e dunque otteniamo la successione

$$\begin{array}{l} F_1x^{(1)}=b \\ F_2x^{(2)}=x^{(1)} \\ ... ... \\ F_px^{(p)}=x^{(p-1)} \\ x \equiv x^{(p)} \end{array}$$

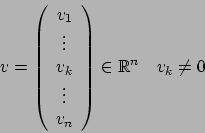
Abbiamo così ridotto il problema iniziale $Ax=b$ nel trovare una fattorizzazione di $A$ e risolvere poi i corrispondenti sistemi lineari.