Next: Il metodo di eliminazione Up: Fattorizzazione Previous: Fattorizzazione Indice
Cerchiamo di risolvere il nostro problema della fattorizzazione
risolvendone prima uno più semplice: dato un vettore
Definiamo allora un vettore, detto vettore elementare di Gauss nel seguente modo:
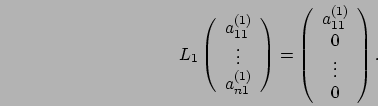 e dunque il loro prodotto sarà una matrice
e dunque il loro prodotto sarà una matrice 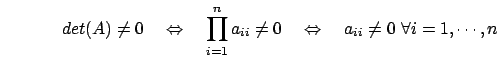 le cui colonne saranno tutte nulle tranne la k-esima che contiene
il vettore
le cui colonne saranno tutte nulle tranne la k-esima che contiene
il vettore 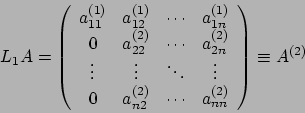
Una matrice siffatta si dice matrice elementare di Gauss, e
soddisfa le nostre richieste, proviamo a verificarlo:
La matrice ![]() è stata trovata solo grazie al fatto che
è stata trovata solo grazie al fatto che ![]() che è condizione necessaria e sufficiente affinchè il problema
abbia soluzione.
che è condizione necessaria e sufficiente affinchè il problema
abbia soluzione.
Vediamo adesso che forma ha la matrice  . Sappiamo per
certo che è triangolare inferiore a diagonale unitaria, ed è
ottenuta come l'identità a cui viene aggiunto lo stesso termine di
correzione di rango uno di
. Sappiamo per
certo che è triangolare inferiore a diagonale unitaria, ed è
ottenuta come l'identità a cui viene aggiunto lo stesso termine di
correzione di rango uno di ![]() :
:
Morpheus 2004-01-04