Next: Requisiti algebrici della fattorizzazione Up: Fattorizzazione Previous: Gauss ci da una Indice
Adesso andremo a compiere la vera e propria fattorizzazione.
Quello che faremo sarà trovare una matrice triangolare superiore
ottenendola da ![]() attraverso opportune trasformazioni.
Innanzitutto poniamo
attraverso opportune trasformazioni.
Innanzitutto poniamo
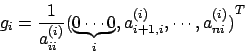
dove con l'indice ![]() stabiliamo l'ultimo passaggio in cui quel
determinato elemento della matrice è stato modificato. In modo
iterativo, al passo i-esimo ci concentreremo sulla colonna i-esima
ed il compito del passo corrente sarà quello di fare in modo che
quella colonna diventi la colonna di una matrice triangolare
superiore e quindi annulli gli elementi dall'(i+1)-esima posizione
in poi.
stabiliamo l'ultimo passaggio in cui quel
determinato elemento della matrice è stato modificato. In modo
iterativo, al passo i-esimo ci concentreremo sulla colonna i-esima
ed il compito del passo corrente sarà quello di fare in modo che
quella colonna diventi la colonna di una matrice triangolare
superiore e quindi annulli gli elementi dall'(i+1)-esima posizione
in poi.
Al primo passo si devono azzerare gli elementi
 , quindi se
, quindi se ![]() possiamo
definire
possiamo
definire
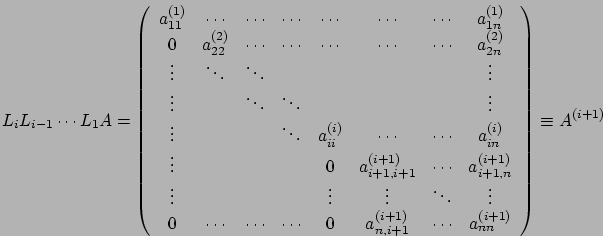
Come si può vedere l'indice all'interno della sottomatrice di ![]() è stato aggiornato: infatti applicando la matrice
è stato aggiornato: infatti applicando la matrice ![]() ad
ad ![]() gli
elementi sulla prima riga rimangono inalterati (il vettore
gli
elementi sulla prima riga rimangono inalterati (il vettore 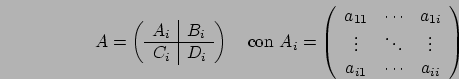 è
stato scelto in modo che lasciasse inalterata proprio la prima
componente del vettore) e si ottiene l'annullamento degli elementi
sotto la diagonale della prima colonna; come effetto secondario
otteniamo la modifica degli elementi della sottomatrice di
è
stato scelto in modo che lasciasse inalterata proprio la prima
componente del vettore) e si ottiene l'annullamento degli elementi
sotto la diagonale della prima colonna; come effetto secondario
otteniamo la modifica degli elementi della sottomatrice di ![]() :
infatti mentre per costruzione della matrice
:
infatti mentre per costruzione della matrice ![]() la prima
colonna viene modificata come volevamo, applicando detta matrice
alle altre colonne, queste verranno modificate senza un preciso
schema, da qui l'aggiornamento dell'indice. Infatti, sia
la prima
colonna viene modificata come volevamo, applicando detta matrice
alle altre colonne, queste verranno modificate senza un preciso
schema, da qui l'aggiornamento dell'indice. Infatti, sia ![]() un
vettore qualsiasi:
un
vettore qualsiasi:
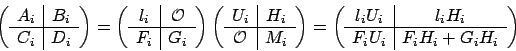
Abbiamo così concluso il primo passo.
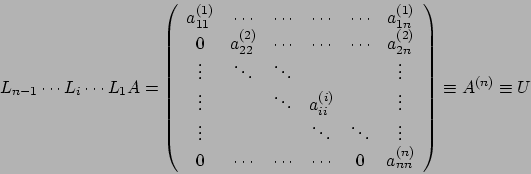
Durante il generico passo i-esimo vediamo come prosegue
l'algoritmo. Se ![]() possiamo definire
possiamo definire
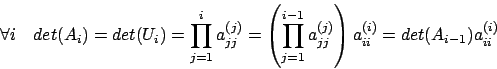
Dopo ![]() passi otteniamo:
passi otteniamo:
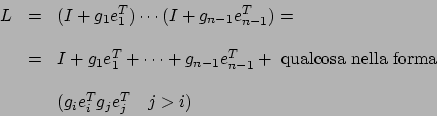
Morpheus 2004-01-04