Costruzione dell'algoritmo di fattorizzazione $LU$

Cerchiamo adesso di costruire un algoritmo per fattorizzare la matrice $A$ come $LU$ prestando particolare attenzione al costo computazionale ed all'occupazione di memoria.

Dal punto di vista dell'occupazione di memoria questo algoritmo risulta particolarmente efficiente perché riusciamo a riscrivere sopra alla matrice $A$ le informazioni necessarie alla fattorizzazione e cioè la parte triangolare superiore di $U$ è la parte strettamente triangolare inferiore di $L$: essendo una matrice a diagonale unitaria non c'è necessità di memorizzarne anche la diagonale. Lo spazio di memoria necessario è dunque quello occupato dalla matrice $A$.

Durante il primo passo vengono azzerati gli elementi $a_{21}^{(1)}\cdots a_{n1}^{(1)}$, possiamo allora utilizzare questi spazi lasciati vuoti per memorizzarci qualcosa. Ricordandoci come abbiamo costruito la matrice elementare di Gauss

$$L_1=I-g_1e_i^T$$

$$\mbox{con } g_1=\frac{1}{a_{11}^{(1)}}{(0a_{21}^{(1)}\cdots a_{n1}^{(1)})}^T$$

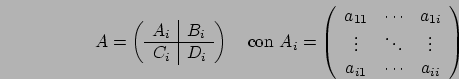le informazioni necessarie per ricostruire $L_1$ sono gli elementi non nulli del vettore $g_1$ che altri non sono che gli elementi da azzerare divisi per l'elemento diagonale, per cui quello che andremo a fare sarà dividere gli elementi in loco per $a_{11}^{(1)}$.

Applicando questo passaggio nella parte strettamente inferiore di $A$ vi otterremo gli elementi non nulli dei vettori $g_i$, che risulterà essere proprio la parte strettamente inferiore di $L$.