Next: Costruzione dell'algoritmo di fattorizzazione Up: Fattorizzazione Previous: Il metodo di eliminazione Indice
Prestiamo attenzione ai requisiti algebrici di questa
fattorizzazione. Scriviamo la matrice A come
Adesso possiamo scrivere
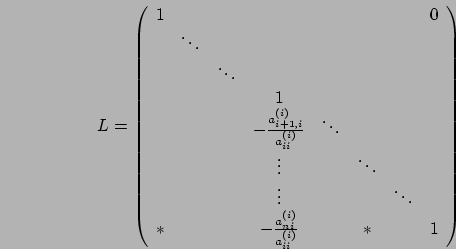 con
con
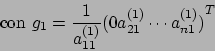
Quanto appena scritto ci consente un'utile interpretazione: la
condizione
![]() ci consente di arrivare fino al
passo i-esimo, mentre
ci consente di arrivare fino al
passo i-esimo, mentre
![]() ci consente di
eseguire proprio il passo i-esimo.
ci consente di
eseguire proprio il passo i-esimo.
La fattorizzazione ![]() è quindi definita se e solo se tutti i
minori principali sono non nulli, e questa è una condizione molto
forte: il problema originario
è quindi definita se e solo se tutti i
minori principali sono non nulli, e questa è una condizione molto
forte: il problema originario ![]() è ben posto solo se il minore
principale di ordine massimo è non nullo (la matrice dei
coefficienti è non singolare). Questo vincolo può essere formulato
sotto forma di teorema che sancisce la condizione necessaria e
sufficiente affinchè la fattorizzazione esista:
è ben posto solo se il minore
principale di ordine massimo è non nullo (la matrice dei
coefficienti è non singolare). Questo vincolo può essere formulato
sotto forma di teorema che sancisce la condizione necessaria e
sufficiente affinchè la fattorizzazione esista:
Guardiamo adesso come è fatta la matrice ![]() . Dall'applicazione
dell'algoritmo precedente quello che otteniamo è
. Dall'applicazione
dell'algoritmo precedente quello che otteniamo è
Questo metodo è detto metodo di eliminazione di Gauss visto l'utilizzo delle matrici e dei vettori elementari dello stesso Gauss
Morpheus 2004-01-04