Next: Gli standard IEEE floating Up: Rappresentazione dei numeri nel Previous: Aritmetica intera Indice
La rappresentazione che solitamente si usa sui calcolatori per i numeri reali è quella floating point, rappresentazione basata sul seguente
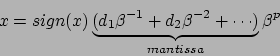
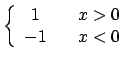
Quella descritta nel teorema prende il nome di forma floating
point normalizzata, in quanto viene richiesto ![]() ; il
fattore
; il
fattore ![]() è detto parte esponenziale e le cifre
è detto parte esponenziale e le cifre ![]() della mantissa sono le cifre significative.
della mantissa sono le cifre significative.
Per poter definire i numeri che apparterranno all'insieme
![]() sarà necessario porre un
intervallo per la caratteristica,
sarà necessario porre un
intervallo per la caratteristica, ![]() e solitamente
e solitamente
![]() e
e ![]() ; inoltre non è possibile rappresentare le infinite
cifre significative dei numeri reali, si fissa allora
; inoltre non è possibile rappresentare le infinite
cifre significative dei numeri reali, si fissa allora ![]() come
massimo numero di cifre significative per un numero che appartiene
all'insieme
come
massimo numero di cifre significative per un numero che appartiene
all'insieme ![]() . Possiamo finalmente definire
. Possiamo finalmente definire
![]() , l'insieme dei numeri macchina, come
, l'insieme dei numeri macchina, come
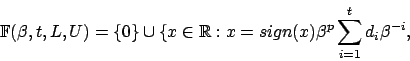
Morpheus 2004-01-04