Next: Matrici simmetriche e definite Up: Matrici sicuramente fattorizzabili Previous: Matrici sicuramente fattorizzabili Indice
In caso di matrici di questo tipo abbiamo la proprietà che ogni
sottomatrice di ordine ![]() ,
, ![]() , è a diagonale dominante:
infatti
, è a diagonale dominante:
infatti
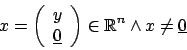
Abbiamo dimostrato che se ![]() è a diagonale dominante, allora tali
sono anche le sue sottomatrici principali; per dimostrare che
è a diagonale dominante, allora tali
sono anche le sue sottomatrici principali; per dimostrare che ![]() è fattorizzabile
è fattorizzabile ![]() quello che dobbiamo dimostrare è che
quello che dobbiamo dimostrare è che ![]() è
non singolare, e cioè che i suoi minori principali sono non nulli.
Dimostriamo dunque che se
è
non singolare, e cioè che i suoi minori principali sono non nulli.
Dimostriamo dunque che se ![]() è a diagonale dominante, allora
è a diagonale dominante, allora ![]() è non singolare.
è non singolare.
Per assurdo supponiamo ![]() essere a diagonale dominante e
singolare, allora esiste
essere a diagonale dominante e
singolare, allora esiste
![]() tale che
tale che
 e questo vettore è definito a meno di una
costante. Assumiamo allora
e questo vettore è definito a meno di una
costante. Assumiamo allora
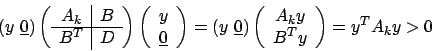
Dunque se una matrice è a diagonale dominante è non singolare ed
allora è fattorizzabile ![]() come si voleva dimostrare.
come si voleva dimostrare.
Morpheus 2004-01-04