Next: Implementazione in Matlab Up: Fattorizzazioni di matrici Previous: Ottenere matrici simmetriche e Indice
Sappiamo che se ![]() è una matrice simmetrica e definita positiva
allora
è una matrice simmetrica e definita positiva
allora ![]() è fattorizzabile
è fattorizzabile ![]() . Ciò che ci proponiamo adesso è
scrivere
. Ciò che ci proponiamo adesso è
scrivere ![]() come
come ![]() con
con ![]() matrice diagonale
matrice diagonale
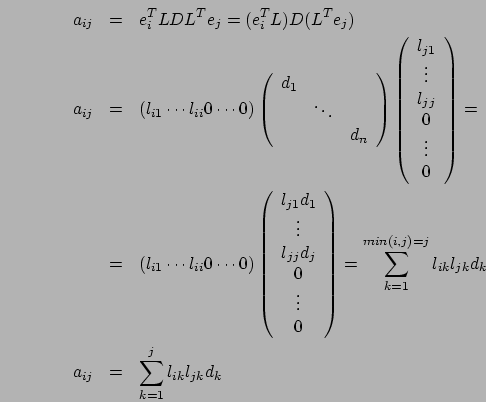 . Posto
. Posto 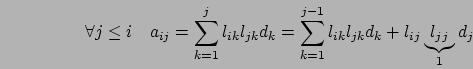 , per la
prima riga si ha
, per la
prima riga si ha
Questo risultato è valido per ogni riga, perciò la matrice
![]() avrà elementi diagonali pari ad uno
avrà elementi diagonali pari ad uno
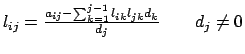 , ma
ciò è garantito dalla possibilità di fattorizzazione
, ma
ciò è garantito dalla possibilità di fattorizzazione 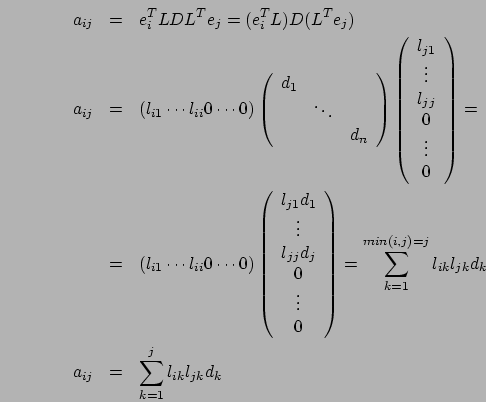 . Unendo le due espressioni sopra otteniamo
. Unendo le due espressioni sopra otteniamo
Perciò se ![]() è simmetrica definita positiva conviene cercare una
fattorizzazione nella forma
è simmetrica definita positiva conviene cercare una
fattorizzazione nella forma ![]() ; la matrice
; la matrice ![]() non ci serve,
necessitiamo solo della sua diagonale e di
non ci serve,
necessitiamo solo della sua diagonale e di ![]() .
.
Quello che ci proponiamo di fare è riorganizzare i passi della
fattorizzazione ![]() senza calcolare
senza calcolare ![]() e supporremo di avere a
disposizione solo la porzione triangolare inferiore di
e supporremo di avere a
disposizione solo la porzione triangolare inferiore di ![]() , in
modo che
, in
modo che
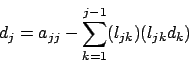
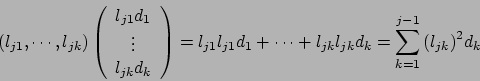
Si presentano dunque due casi:
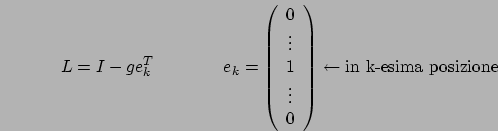
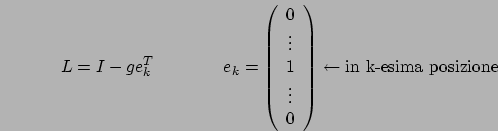
Quindi, durante il primo passo viene calcolato 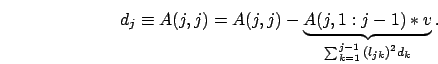 e poi tutta
la prima colonna di
e poi tutta
la prima colonna di ![]() , e poi l'algoritmo procede nello stesso
modo.
, e poi l'algoritmo procede nello stesso
modo.