Next: Congruenza forte Up: La bisimulazione Previous: La bisimulazione Indice
La prima proprietà che vogliamo mostrare è come la strong bisimulation sia preservata da alcune operazioni sulle relazioni (teniamo a mente quanto visto in precedenza su relazioni inverse e composte):
Per qualche ![]() , avremo che
, avremo che
Sia adesso
![]() . Allora per
qualche
. Allora per
qualche ![]() avremo, dal momento che
avremo, dal momento che
![]()
Inoltre, poichè
![]() si ha, per qualche
si ha, per qualche
![]()
Da questo si ottiene
![]() . In modo del tutto simile si trova che
se
. In modo del tutto simile si trova che
se
![]() , allora possiamo
trovare un
, allora possiamo
trovare un ![]() tale che
tale che
![]() e
e
![]() .
.
![]()
Dimostriamo due proprietà accennate in precedenza ma che non abbiamo provato:
Riflessività:
![]() dal punto 1.
della proposizione 6.1;
dal punto 1.
della proposizione 6.1;
Simmetria: se
![]() allora
allora
![]() per qualche bisimulazione forte
per qualche bisimulazione forte
![]() . Allora
. Allora
![]() e quindi
e quindi
![]() per il
punto 2. della proposizione 6.1;
per il
punto 2. della proposizione 6.1;
Transitività: se
![]() e se
e se
![]() allora
allora
![]() e
e
![]() per
qualche bisimulazione forte
per
qualche bisimulazione forte
![]() ed
ed
![]() .
Dunque
.
Dunque
![]() e quindi
e quindi
![]() per il punto 3. della proposizione 6.1.
per il punto 3. della proposizione 6.1.
Vogliamo dunque provare che ![]() soddisfa le proprietà che
abbiamo chiamato (
soddisfa le proprietà che
abbiamo chiamato (![]() ). Sappiamo che metà dell'implicazione
vale, in quanto 'sse' è stato rimpiazzato da 'implica', dal
momento che
). Sappiamo che metà dell'implicazione
vale, in quanto 'sse' è stato rimpiazzato da 'implica', dal
momento che ![]() è una bisimulazione forte; rimane dunque da
provare l'altra metà. Per fare questo, definiamo dapprima una
nuova relazione,
è una bisimulazione forte; rimane dunque da
provare l'altra metà. Per fare questo, definiamo dapprima una
nuova relazione, ![]() in termini di
in termini di ![]() nel modo seguente:
nel modo seguente:
Dalla proposizione 6.2, punto 1., sappiamo che ![]() è una bisimulazione forte, possiamo allora dedurre che
è una bisimulazione forte, possiamo allora dedurre che
Rimane da provare il viceversa, cioè che
![]() implica
implica
![]() . Il seguente risultato è sufficiente:
. Il seguente risultato è sufficiente:
Si è quindi dimostrato che ![]() soddisfa (
soddisfa (![]() ):
):
Quello che vogliamo fare è provare che molte delle leggi di
inferenza introdotte per CCS possono essere provare vere se si
interpreta '=' come la bisimulazione forte; quanto proveremo
adesso risulta valido anche per la nozione di bisimulazione debole
(più generosa). In ogni caso, le ![]() laws non sono valide per
la bisimulazione forte ma soltanto per la nozione debole.
laws non sono valide per
la bisimulazione forte ma soltanto per la nozione debole.
Per questo punto, abbiamo bisogno di mostrare che
![]() è
una bisimulazione forte, dove
è
una bisimulazione forte, dove
Supponiamo ora che
![]() . Ci sono tre casi, con
relativi sottocasi, che possono verificarsi:
. Ci sono tre casi, con
relativi sottocasi, che possono verificarsi:
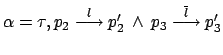 e
e
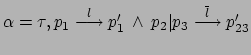 e
e
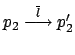 e
e
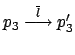 e
e
Questo prova la condizione 1. della definizione 5.9;
la condizione 2. segue da un'argomentazione simmetrica, ed abbiamo
così mostrato che
![]() è una strong bisimulation.
è una strong bisimulation.
Le altre parti della proposizione sono trattate in maniera simile.
Per 4. si deve provare che, per un fissato ![]() , la relazione
, la relazione
è una bisimulazione forte. Ora, se
![]() , allora (per la condizione sopra)
, allora (per la condizione sopra)
![]() implica che
implica che
![]() ; rimane da mostrare che
; rimane da mostrare che
![]() . Ma
. Ma
![]() per ogni
per ogni ![]() derivazione di
derivazione di ![]() , così
, così
![]() , e di
conseguenza
, e di
conseguenza
![]() come
richiesto.
come
richiesto.
Le restanti parti non introducono altre problematiche.
![]()
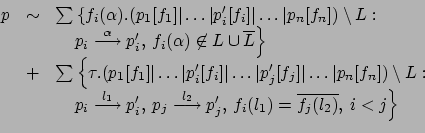
Se
![]() , allora
, allora
![]() (
(![]() )
)
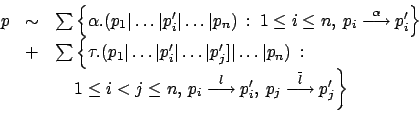
Per ![]() ci si riduce a provare che
ci si riduce a provare che
![]() , il che è immediato. Assumiamo vero il risultato per
, il che è immediato. Assumiamo vero il risultato per ![]() e
consideriamo
e
consideriamo
![]() . E' immediato,
dall'applicazione delle regole di Composizione parallela che
. E' immediato,
dall'applicazione delle regole di Composizione parallela che
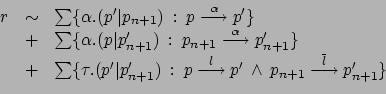
Usiamo ora l'assunzione iniziale per
![]() , allora la parte destra può essere riformulata ne
modo seguente (si noti che la prima sommatoria può essere divisa
in due parti, a seconda che
, allora la parte destra può essere riformulata ne
modo seguente (si noti che la prima sommatoria può essere divisa
in due parti, a seconda che
![]() sia dovuto ad un singolo
sia dovuto ad un singolo ![]() oppure all'interazione tra
oppure all'interazione tra
![]() e
e ![]() ):
):
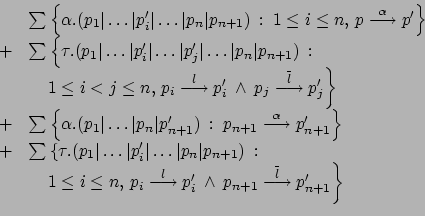
Possiamo allora ricombinare la prima con la terza sommatoria e la seconda con la quarta per ottenere quanto si cercava:
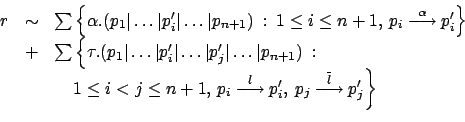
Possiamo dunque estendere (![]() ) per provare il teorema nella
forma in cui è stato enunciato. Possiamo introdurre per prima il
Relabelling, considerando
) per provare il teorema nella
forma in cui è stato enunciato. Possiamo introdurre per prima il
Relabelling, considerando
![]() in (
in (![]() ), ed
osservando che
), ed
osservando che ![]() ha una transizione
ha una transizione
![]() sse
sse ![]() ha una
transizione
ha una
transizione
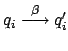 tale che
tale che
![]() e
e
![]() . Possiamo infine
introdurre la Restrizione, usando l'equivalenza forte
. Possiamo infine
introdurre la Restrizione, usando l'equivalenza forte
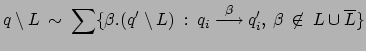
dove
![]() .
.
![]()
Abbiamo quindi dimostrato tutte le leggi viste sostitudendo al
simbolo '=' quello di bisimulazione forte '![]() '. Ciò che adesso
vogliamo fare è provare che
'. Ciò che adesso
vogliamo fare è provare che ![]() è una relazione di congruenza,
cioè che se due processi sono bisimili fortemente, allora dove ce
n'è uno si può sostituire l'altro.
è una relazione di congruenza,
cioè che se due processi sono bisimili fortemente, allora dove ce
n'è uno si può sostituire l'altro.