Next: Bisimulazione debole Up: Bisimulazione forte Previous: Bisimulazione forte Indice
Ora vogliamo mostrare che la bisimualzione forte è una congruenza
Dimostriamo dunque che la bisimulazione forte è sostituitiva per tutti i combinatori:
La prova per 2. è simile.
Per 3., invece, si deve mostrare che
![]() è una
bisimulazione, dove
è una
bisimulazione, dove
Supponiamo allora che
![]() . Sia
. Sia
![]() . Ci sono tre casi
possibili:
. Ci sono tre casi
possibili:
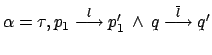 e
e
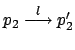 con
con
Le prove per 4. e 5. sono simili.
![]()
Morpheus 2004-02-10