Next: Congruenza debole Up: La bisimulazione Previous: Congruenza forte Indice
Come fatto per la bisimulazione forte, intendiamo ora dimostrare proprietà analoghe anche per la bisimulazione debole.
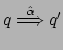 allora, per
qualche
allora, per
qualche
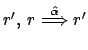 e
e
Continuando con l'analogia, vogliamo dunque provare che ![]() soddisfa (
soddisfa (
![]() ): definiamo dunque una nuova relazione,
): definiamo dunque una nuova relazione,
![]() in termini di
in termini di ![]() nel modo seguente:
nel modo seguente:
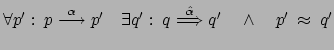
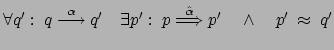 .
.
Dalla proposizione 6.2, punto 1., sappiamo che
![]() è una bisimulazione debole, e possiamo dedurre
similmente che
è una bisimulazione debole, e possiamo dedurre
similmente che
![]() implica
implica
![]() ,
rimane da provare che
,
rimane da provare che
![]() implica
implica
![]() :
:
Abbiamo dunque dimostrato che ![]() soddisfa (
soddisfa (
![]() ),
cioè che:
),
cioè che:
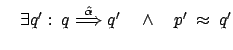
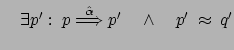
Presentiamo ancora ulteriori proprietà della bisimulazione, e
guardiamo proprio al caso emblematico che la distingue da ![]() :
:
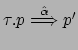 , e sappiamo che
, e sappiamo che
Quello che abbiamo dimostrato è proprio la potenza della
bisimulazione: consente di ignorare le azioni ![]() durante
l'investigazione sulla bisimilarità! Purtroppo però, proprio a
causa della prelazione dell'azione
durante
l'investigazione sulla bisimilarità! Purtroppo però, proprio a
causa della prelazione dell'azione ![]() , la bisimulazione non è
preservata dalla Somma, come si vede da questo esempio:
, la bisimulazione non è
preservata dalla Somma, come si vede da questo esempio:
Per questo, la nozione di '![]() ' non è quella di uguaglianza
'=', ma le due nozioni sono molto vicine: vedremo in seguito come
un modifica minima nella definizione di
' non è quella di uguaglianza
'=', ma le due nozioni sono molto vicine: vedremo in seguito come
un modifica minima nella definizione di ![]() li renda
concetti equivalenti.
li renda
concetti equivalenti.
Da questo risultato, sembra che la differenza tra bisimulazione ed
uguaglianza stia esclusivamente nella presenza di azioni ![]() iniziali. Il seguente risultato lo evidenzia ancora maggiormente:
iniziali. Il seguente risultato lo evidenzia ancora maggiormente:
Questo implica che la bisimulazione viene preservata dalla Sequenzalizzazione (in questo caso è addirittura rafforzata!) e da tutti gli altri operatori ad eccezione della Somma.