Next: Assiomatizzazione della bisimulazione Up: Bisimulazione debole Previous: Bisimulazione debole Indice
Ciò che si vuole individuare è la più grande relazione di
congruenza che includa ![]() . Per fare questo, inizieremo
definendo in modo differente la nozione di bisimulazione e
proveremo che la bisimulazione è preservata per tutti i
combinatori ad eccezione della Somma. Daremo infine la definizione
di uguaglianza '=' e vedremo che questa è effettivamente una
relazione di congruenza, che giustifica tutte le normali
manipolazioni algebriche (la sostituzione di uguali per uguali).
Mostreremo come le
. Per fare questo, inizieremo
definendo in modo differente la nozione di bisimulazione e
proveremo che la bisimulazione è preservata per tutti i
combinatori ad eccezione della Somma. Daremo infine la definizione
di uguaglianza '=' e vedremo che questa è effettivamente una
relazione di congruenza, che giustifica tutte le normali
manipolazioni algebriche (la sostituzione di uguali per uguali).
Mostreremo come le ![]() laws valgano ed infine mostreremo un
insieme di assiomi che sono completi (dai quali tutte le equazioni
valide possono essere derivate) per i processi finiti ed a stati
finiti.
laws valgano ed infine mostreremo un
insieme di assiomi che sono completi (dai quali tutte le equazioni
valide possono essere derivate) per i processi finiti ed a stati
finiti.
Abbiamo visto in precedenza il concetto di bisimulazione, ed in
particolare la più larga relazione di bisimulazione ![]() , che
abbiamo chiamato equivalenza osservazionale o bisimiliarità.
Iniziamo ora a dare una caratterizzazione alternativa di
bisimulazione in termini di esperimenti. Consideriamo
, che
abbiamo chiamato equivalenza osservazionale o bisimiliarità.
Iniziamo ora a dare una caratterizzazione alternativa di
bisimulazione in termini di esperimenti. Consideriamo
![]() , dove
, dove
![]() , un esperimento su
, un esperimento su ![]() : consiste nell'eseguire
: consiste nell'eseguire ![]() per un po' ed osservare la sequenza
per un po' ed osservare la sequenza
![]() .Se
.Se
![]() , scriveremo
, scriveremo
![]() (se, cioè,
(se, cioè, ![]() non è stabile, ciò può essere dovuto ad una o più azioni
non è stabile, ciò può essere dovuto ad una o più azioni ![]() ).
).
![]() è comunque un esperimento, dal momento che
è comunque un esperimento, dal momento che ![]() ammette meno esperimenti di
ammette meno esperimenti di ![]() : ad esempio,
: ad esempio,
![]() ammette l'esperimento
ammette l'esperimento ![]() , ma possiamo fare
, ma possiamo fare
![]() e quest'ultimo non ammette un esperimento
e quest'ultimo non ammette un esperimento ![]() .
.
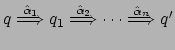 con
con
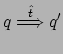 , e quindi
, e quindi
(
![]() ) Assumendo 1., sia
) Assumendo 1., sia
![]() . Se
. Se
![]() allora
allora
![]() e così da 1. si ha
e così da 1. si ha
![]() con
con
![]() ; ma
; ma
![]() , quindi
, quindi
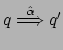 come richiesto. Se
come richiesto. Se
![]() allora
allora
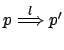 , e grazie
a 1.
, e grazie
a 1.
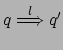 con
con
![]() ; ma
; ma ![]() e quindi
e quindi
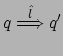 come richiesto. Assumendo
2., similmente si deriva la seconda condizione per la
bisimulazione.
come richiesto. Assumendo
2., similmente si deriva la seconda condizione per la
bisimulazione.
![]()
Il motivo per includere l'esperimento vuoto
![]() nella proposizione di sopra è che, senza di esso, avremmo che
nella proposizione di sopra è che, senza di esso, avremmo che
![]() certamente falso nella nostra
definizione originaria.
certamente falso nella nostra
definizione originaria.
Guardiamo ora alla sostitutività di ![]() . Abbiamo già
accennato al fatto che, in generale,
. Abbiamo già
accennato al fatto che, in generale, ![]() non è preservata da
Somma:
non è preservata da
Somma:
mentre
D'altro canto, abbiamo che Prefix rafforza la bisimilarità verso l'uguaglianza; per ora ci limitiamo a dimostarare che:
è una bisimulazione. Sia allora
![]() (dal momento che tutte
le derivazioni devono avere questa forma).
(dal momento che tutte
le derivazioni devono avere questa forma).
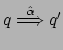 per qualche
per qualche
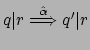 e dunque
e dunque
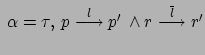
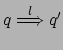 per qualche
per qualche
Da questo, tramite un argomento simmetrico, si ottiene che
![]() è una bisimulazione.
è una bisimulazione.
![]()
Quanto detto vale poichè l'azione invisibile ![]() non può mai
essere ristretta o rinominata.
non può mai
essere ristretta o rinominata.
Come appena mostrato, la bisimulazione non è completamente
sostitutiva (
![]() non implica
non implica
![]() ), mentre noi cerchiamo una nozione di uguaglianza,
), mentre noi cerchiamo una nozione di uguaglianza, ![]() ,
che implichi
,
che implichi
![]() e che sia completamente
sostitutiva: cerchiamo una relazione di congruenza, che sia la più
larga relazione a contenere
e che sia completamente
sostitutiva: cerchiamo una relazione di congruenza, che sia la più
larga relazione a contenere ![]() .
.
Si noti la somiglianza con la definizione di bisimulazione:
infatti, differiscono soltanto in un aspetto, e cioè qui abbiamo
![]() al posto di
al posto di
![]() . Questo implica che ogni
azione di
. Questo implica che ogni
azione di ![]() o
o ![]() deve essere corrisposta da almeno una azione
dell'altro processo. Si noti inoltre come questo si applichi solo
all'azione iniziale, in quanto poi si richiede che
deve essere corrisposta da almeno una azione
dell'altro processo. Si noti inoltre come questo si applichi solo
all'azione iniziale, in quanto poi si richiede che
![]() e non
e non ![]() .
.
Guardiamo un risultato interessante, che ci mostra come le nozioni
di uguaglianza e bisimilarità siano molto vicine (l'ipotesi che
faremo è che si possa sempre costruire un nuovo nome
indipendentemente da quanti se ne sono usati finora indicando con
![]() il linguaggio generato da
il linguaggio generato da ![]() e con
e con
![]() il linguaggio di tutta la nostra algebra)
il linguaggio di tutta la nostra algebra)
(
![]() ) Proviamo il contropositivo. Supponiamo dunque che
) Proviamo il contropositivo. Supponiamo dunque che
![]() . Allora, per esempio, avremo che ci sono
. Allora, per esempio, avremo che ci sono ![]() e
e
![]() tali che
tali che
![]() ma che per
qualsiasi
ma che per
qualsiasi
![]() si ha
si ha
![]() . Scegliamo ora
. Scegliamo ora
![]() , dove
, dove ![]() non è nel
linguaggio di
non è nel
linguaggio di ![]() o di
o di ![]() . Chiaramente
. Chiaramente
![]() ; si deve allora mostrare
che qualsiasi
; si deve allora mostrare
che qualsiasi
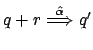 si ha
si ha
![]() . Se
. Se
![]() e
e
![]() ,
allora
,
allora
![]() in quanto
in quanto ![]() ha un'azione
ha un'azione ![]() che
che
![]() non ha; d'altra parte
non ha; d'altra parte
![]() e quindi
e quindi
![]() (in quanto
(in quanto
![]() è impossibile dal
momento che
è impossibile dal
momento che
![]() ), e quindi ancora
), e quindi ancora
![]() .
.
![]()
Vediamo ora come l'uguaglianza si trovi nel mezzo tra congruenza forte e bisimilarità:
Per quanto riguarda la seconda parte, dalla proprosizione sopra
abbiamo che ![]() implica
implica
![]() , ma
, ma
![]() e quindi
e quindi
![]() , da cui segue
, da cui segue
![]() .
.
![]()
Quindi, tutte le leggi valide per ![]() e = lo sono anche per la
bisimilarità, mentre non vale il viceversa: abbiamo che
e = lo sono anche per la
bisimilarità, mentre non vale il viceversa: abbiamo che
![]() mentre in generale abbiamo
mentre in generale abbiamo
![]() .
.
Facciamo il primo passo per dimostrare che l'uguaglianza è una congruenza mostrando che:
Vediamo come, attraverso la Sequenzalizzazione, si rafforzi la bisimilarità verso la uguaglianza, già osservato nella sezione precedente:
Si deve ora provare che tutti gli operatori preservano l'ugaglianza:
Le rimanenti prove sono applicazioni dirette della definizione di
uguaglianza. Per la Composizione parallela, un'analisi a casi come
nella proposizione 6.15 è necessaria; le altre due
sono più dirette.
![]()
Raccogliendo tutti i risultati ottenuti si arriva a poter affermare che l'uguaglianza è una congruenza.
Avevamo lasciato in sospeso alcune proprietà, che ora riprendiamo dimostrando:
Mostriamo anche che
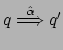 con
con
Proviamo infine un risultato tanto inatteso quanto importante e che mostra ancora una volta come la nozione di bisimilarità e di uguaglianza siano vicine; questo risultato venne per la prima volta provato da Matthew Hennessey e verrà poi sfruttato in seguito per provare la completezza dell'insieme di assiomi che introdurremo:
(
![]() ) Assumiamo
) Assumiamo
![]() , e consideriamo i
tre casi possibili. Primo, supponiamo che
, e consideriamo i
tre casi possibili. Primo, supponiamo che
![]() per qualche
per qualche
![]() ; è facile vedere allora come
; è facile vedere allora come
![]() . Secondo,
supponiamo che
. Secondo,
supponiamo che
![]() per qualche
per qualche ![]() ; in modo simile si mostra che
; in modo simile si mostra che
![]() .
Se nessuna delle due condizioni si è verificata, allora si può
mostrare che
.
Se nessuna delle due condizioni si è verificata, allora si può
mostrare che ![]() nel modo seguente: consideriamo dapprima che
nel modo seguente: consideriamo dapprima che
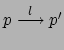 ; dal momento che
; dal momento che
![]() abbiamo che
abbiamo che
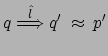 , e cioè
, e cioè
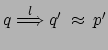 come richiesto. Nell'altro caso, e cioè se
come richiesto. Nell'altro caso, e cioè se
![]() allora
allora
![]() , e
, e ![]() non può essere
non può essere ![]() stesso per ipotesi e
quindi
stesso per ipotesi e
quindi
![]() come richiesto. Grazie alla simmetria segue che
come richiesto. Grazie alla simmetria segue che ![]() .
.
![]()
Quanti abbiamo fatto in questa sezione è stato trovare una nozione di uguaglianza completamente sostitutiva e molto vicina alla bisimilarità; a questo punto potremmo obiettare che la bisimilarità è quasi ridondante. Invece, le dimostrazioni che stabiliscono una bisimilarità sono molto convenienti, ed inoltre, stabilire una bisimilarità è molto naturale ed a volte anche meccanizzabile.
Morpheus 2004-02-10