Next: Testing equivalence Up: La bisimulazione Previous: Congruenza debole Indice
E' chiaro che attraverso l'expansion law, ogni processo finito può essere uguagliato ad uno che non contiene Composizione parallela, Restrizioni o Relabelling.
Dunque, attraverso l'expansion law ogni processo può essere uguagliato ad un processo seriale.
Definiamo ora due insiemi di assiomi, uno per Somme ed uno per Sequenzalizzazione:
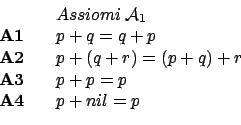
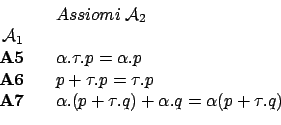
Sappiamo già che la seguente è conseguenza di
![]() :
:
Con l'aiuto dell'expansion law ogni equazione valida tra processi
finiti segue da
![]() : questo significa che abbiamo una
completa assiomatizzazione per i processi finiti, e questo
significa che possiamo mostrare che
: questo significa che abbiamo una
completa assiomatizzazione per i processi finiti, e questo
significa che possiamo mostrare che
![]() sono corretti
e completi per processi finiti seriali.
sono corretti
e completi per processi finiti seriali.
In quello che segue useremo ![]() per indicare che
per indicare che ![]() e
e ![]() sono
uguali per la definizione 6.4 di uguaglianza, mentre
sono
uguali per la definizione 6.4 di uguaglianza, mentre
![]() intendiamo dire che l'uguaglianza può
essere provata da un ragionamento equazionale dagli assiomi
intendiamo dire che l'uguaglianza può
essere provata da un ragionamento equazionale dagli assiomi
![]() ; useremo
; useremo ![]() per l'identità sintattica.
per l'identità sintattica.
Consideriamo la potenza dell'insieme
![]() :
:
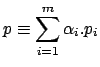
dove ogni ![]() è anch'esso in standard form.
è anch'esso in standard form.
Si vede che nil è in s.f.: è il caso limite ![]() . Inoltre, si
noti come l'ordine degli addendi possa essere ignorato grazie agli
assiomi
. Inoltre, si
noti come l'ordine degli addendi possa essere ignorato grazie agli
assiomi ![]() ed
ed ![]() .
.
Il risultato seguente è molto importante e mostra come
![]() sia corretto e completo rispetto alla nozione di
strong congruence.
sia corretto e completo rispetto alla nozione di
strong congruence.
(
![]() ) Completezza. Assumiamo
) Completezza. Assumiamo
![]() ed inoltre
che
ed inoltre
che ![]() e
e ![]() siano entrambi in standard form, cioè della forma
siano entrambi in standard form, cioè della forma
![]() e
e
![]() . Proveremo la proposizione per induzione
sull'altezza massima di
. Proveremo la proposizione per induzione
sull'altezza massima di ![]() e
e ![]() , dove l'altezza di
, dove l'altezza di ![]() è
definita come il massimo numero di Sequenzalizzazioni innestate in
è
definita come il massimo numero di Sequenzalizzazioni innestate in
![]() .
.
Se la massima profondità è pari a zero, allora entrambi i processi
sono nil (in quanto entrambi in standard form) ed il ragionamento
equazionale ci garantisce che che
![]() (la riflessività è parte del ragionamento equazionale).
(la riflessività è parte del ragionamento equazionale).
In caso contrario, sia ![]() un sommando di
un sommando di ![]() . Allora
. Allora
![]() , e dal fatto che
, e dal fatto che
![]() , esiste un certo
, esiste un certo ![]() tale che
tale che
![]() . Poichè
. Poichè ![]() è
in standard form, allora
è
in standard form, allora ![]() è un sommando di
è un sommando di ![]() e per
induzione
e per
induzione
![]() e quindi il sommando
e quindi il sommando
![]() di
di ![]() può essere provato uguale ad un sommando di
può essere provato uguale ad un sommando di
![]() . Similmente, ogni sommando
. Similmente, ogni sommando ![]() di
di ![]() può essere
provato uguale ad un sommando di
può essere
provato uguale ad un sommando di ![]() . Segue dunque che
. Segue dunque che
![]() , usando l'assioma
, usando l'assioma ![]() per
eliminare i sommandi duplicati (e gli assiomi
per
eliminare i sommandi duplicati (e gli assiomi ![]() ed
ed ![]() per riordinare e raggruppare i sommandi, ove necessario).
per riordinare e raggruppare i sommandi, ove necessario).
![]()
Possiamo pensare alla f.s.f. come 'saturata' nel seguente senso:
per ogni
![]() allora
allora
![]() appare come un sommando di
appare come un sommando di ![]() . Vedremo ora come ogni
s.f. può essere saturata utilizzando
. Vedremo ora come ogni
s.f. può essere saturata utilizzando
![]()


e questo completa la prova.
![]()
Con l'aiuto di questo lemma, possiamo trasformare ogni s.f. in una f.s.f. equivalente:
è in f.s.f. di uguale profondità di ![]() , e grazie al lemma di
saturazione,
, e grazie al lemma di
saturazione,
![]() .
.
![]()
Siamo adesso in grado di dimostrare un risultato importante di
questa sezione, cioè che
![]() è corretto e completo per
la nozione di uguaglianza su processi finiti seriali:
è corretto e completo per
la nozione di uguaglianza su processi finiti seriali:
(
![]() ) Completezza. Possiamo assumere che
) Completezza. Possiamo assumere che ![]() e
e ![]() siano
in f.s.f.; la prova procederà per induzione sulla somma delle
profondità di
siano
in f.s.f.; la prova procederà per induzione sulla somma delle
profondità di ![]() e
e ![]() .
.
Quando la somma è pari a zero, allora si ha
![]() , ed il risultato è banale. In caso contrario assumiamo
, ed il risultato è banale. In caso contrario assumiamo ![]() , e
sia
, e
sia ![]() un sommando di
un sommando di ![]() . Miriamo a provare che
. Miriamo a provare che ![]() ha
un sommando provabilmente uguale ad
ha
un sommando provabilmente uguale ad ![]() . Ora
. Ora
![]() , quindi esiste un
, quindi esiste un ![]() tale che
tale che
![]() e
e
![]() . Di più,
. Di più,
![]() in quanto
in quanto
![]() è in f.s.f., e quindi
è in f.s.f., e quindi ![]() è un sommando di
è un sommando di ![]() .
.
Non possiamo applicare immediatamente l'induzione, in quanto
sappiamo soltanto che
![]() e non
e non ![]() . Ma
dall'Hennessey theorem (proposizione 6.23)
sappiamo che allora
. Ma
dall'Hennessey theorem (proposizione 6.23)
sappiamo che allora ![]() o
o
![]() o
o
![]() .
.
Nel primo caso, dal momento che ![]() e
e ![]() sono in f.s.f. e di
profondità minore di
sono in f.s.f. e di
profondità minore di ![]() e
e ![]() , per induzione
, per induzione
![]() , quindi
, quindi
![]() .
Nel secondo caso dobbiamo dapprima convertire
.
Nel secondo caso dobbiamo dapprima convertire ![]() in f.s.f.
prima di poter applicare l'induzione. Dal lemma precedente esiste
un
in f.s.f.
prima di poter applicare l'induzione. Dal lemma precedente esiste
un ![]() in f.s.f. di uguale profondità di
in f.s.f. di uguale profondità di ![]() , tale che
, tale che
![]() ; ma la somma delle profondità
di
; ma la somma delle profondità
di ![]() e
e ![]() e minore di uno della somma delle profondità di
e minore di uno della somma delle profondità di
![]() e
e ![]() , e quindi per induzione possiamo inferire che
, e quindi per induzione possiamo inferire che
![]() e quindi
e quindi
![]() e grazie all'assioma
e grazie all'assioma ![]() si ha che
si ha che
![]() . Il terzo caso è simile a questo.
. Il terzo caso è simile a questo.
Dunque, in ognuno dei tre casi, abbiamo mostrato che da
![]() ogni sommando di
ogni sommando di ![]() di
di ![]() può essere
provato uguale ad un sommando di
può essere
provato uguale ad un sommando di ![]() . In modo simile, ogni
sommando
. In modo simile, ogni
sommando ![]() di
di ![]() può essere provato uguale ad un
sommando di
può essere provato uguale ad un
sommando di ![]() . In fine, utilizzando l'assioma
. In fine, utilizzando l'assioma ![]() per eliminare
gli eventuali sommandi duplicati, possiamo concludere che
per eliminare
gli eventuali sommandi duplicati, possiamo concludere che
![]()
![]()
Morpheus 2004-02-10