Seguendo sempre la linea applicata per la bisimulazione, cerchiamo
ora un'insieme di assiomi corretto e completo rispetto alla
nozione di testing equivalence. Prima di fare questo, vediamo le
relazione tra questa nuova equivalenza e proprio la bisimulazione
debole:
Teorema 7..1
Dati due processi 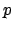 e
e 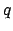 tali che
tali che
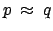 , questo
implica
, questo
implica
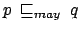 .
.
Dimostrazione.
Dimostriamo l'implicazione inversa delle negazioni, e cioè:
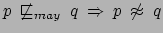
.
Secondo la definizione alternativa di
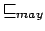 si ha:
si ha:
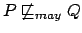
implica che
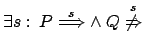
Procediamo dunque per induzione sulla struttura di 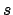 :
:
- Caso base: s=a
Sostituiamo questa ipotesi nella relazione scritta sopra e si
ottiene
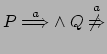 . Si possono allora distinguere due
casi per
. Si possono allora distinguere due
casi per
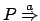 :
:
-
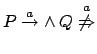 .
.
Ma dalla definizione di 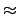 si ottiene che
si ottiene che
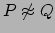 .
.
-
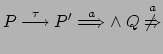 .
.
Dimostriamo dunque la tesi per induzione sulla somma delle profondità di
P e Q. Ci troviamo difronte a tre casi per
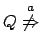 :
:
- a)
-
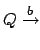 con
con 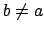 .
.
Essendo 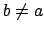 per definizione di bisimulazione si ha
direttamente
per definizione di bisimulazione si ha
direttamente
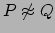 .
.
- b)
-
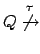 .
.
Quindi si ha che
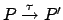 e
e
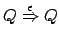 . Assumiamo per assurdo
. Assumiamo per assurdo
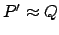 , allora per definizione si avrebbe
, allora per definizione si avrebbe
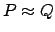 . Ma per
induzione interna, la somma delle profondità di
. Ma per
induzione interna, la somma delle profondità di 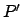 e Q è
minore di 1 rispetto a quella di P e Q, per cui si otterrebbe l'assurdo
e Q è
minore di 1 rispetto a quella di P e Q, per cui si otterrebbe l'assurdo
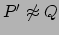 .
.
Anche in questo caso si ottiene che
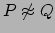 .
.
- c)
-
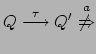 .
.
Avremmo quindi
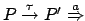 . La somma delle profondità di
. La somma delle profondità di 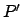 e
e 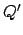 è inferiore di 2 rispetto a quella di P e Q, perciò
applicando l'ipotesi induttiva interna otteniamo che
è inferiore di 2 rispetto a quella di P e Q, perciò
applicando l'ipotesi induttiva interna otteniamo che
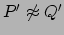 , da cui, nuovamente, che
, da cui, nuovamente, che
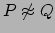 .
.
- Passo induttivo:
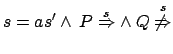 .
.
Quindi, si ha
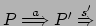 . Si devono prendere in considerazione
due casi:
. Si devono prendere in considerazione
due casi:
-
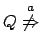 .
.
Si può riapplicare il caso base.
-
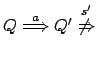 .
.
Applicando l'ipotesi induttiva per 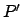 e
e 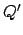 e si ha
e si ha
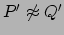 , da cui si ottiene
, da cui si ottiene
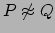 .
.

Dimostriamo un teorema simile anche per il preordine di
must:
Teorema 7..2
Dati due processi 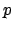 e
e 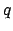 tali che
tali che
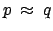 , questo
implica
, questo
implica
 .
.
Dimostrazione.
La dimostrazione segue il metodo visto in precedenza: vedremo cioè
che
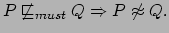
Secondo la definizione alternativa di
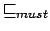 si ha:
si ha:
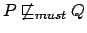
implica che
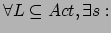
dove con 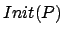 intendiamo l'insieme delle azioni iniziali che
il processo
intendiamo l'insieme delle azioni iniziali che
il processo 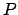 può compiere.
può compiere.
Quanto scritto sopra significa che esiste un processo 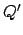 che non
può fare nessuna azione di L, mentre P ne può fare almeno una: sia
questa azione
che non
può fare nessuna azione di L, mentre P ne può fare almeno una: sia
questa azione 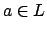 . Quindi
. Quindi
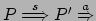 e
e
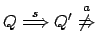 . Da cui si ricava
. Da cui si ricava
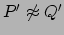 e di conseguenza
e di conseguenza
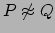 .
.

Possiamo facilmente mostrare che:
Teorema 7..3
Dati due processi 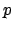 e
e 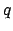 tali che
tali che
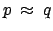 , questo
implica
, questo
implica
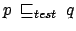 .
.
Dimostrazione.
La prova è immediata: dalla definizione di
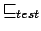
e
dai due precedenti teoremi la tesi è banalmente verificata.

I tre risultati precedenti sono molto importanti per la
correttezza dell'assiomatizzazione che andiamo cercando, in quanto
provano che gli assiomi per la bisimulazione debole sono validi
anche per i preordini della testing equivalence.
Subsections
Morpheus
2004-02-10
![]() si ha:
si ha:
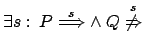
![]() :
:
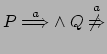 . Si possono allora distinguere due
casi per
. Si possono allora distinguere due
casi per
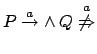 .
.
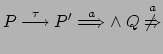 .
.
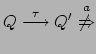 .
.
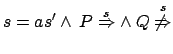 .
.
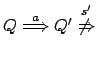 .
.
![]()
![]() si ha:
si ha:
![]() intendiamo l'insieme delle azioni iniziali che
il processo
intendiamo l'insieme delle azioni iniziali che
il processo ![]() può compiere.
può compiere.
![]() che non
può fare nessuna azione di L, mentre P ne può fare almeno una: sia
questa azione
che non
può fare nessuna azione di L, mentre P ne può fare almeno una: sia
questa azione ![]() . Quindi
. Quindi
![]() e
e
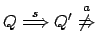 . Da cui si ricava
. Da cui si ricava
![]() e di conseguenza
e di conseguenza
![]() .
.
![]()