
| Figure 3.1: Rappresentazione dell’allocazione di memoria di z |



Si discuteranno qui alcune scelte implementative ed alcuni accorgimenti adottati nell’implementazione del metodo di Wassing.
Come descritto in precedenza la matrice Z è memorizzata in un vettore, chiamato z, il quale contiene esclusivamente gli elementi di Z necessari ai passi successivi. Questi elementi sono memorizzati per colonne:

Figure 3.1: Rappresentazione dell’allocazione di memoria di z
dove con Zi si è indicata l’i-esima colonna di Z.
Gli elementi in questo vettore sono letti e successivametne modificati: al passo i-esimo si ha bisogno di accedere agli elementi della sotto-matrice di Z di indici (i… n+1,1… i−1) che sono già presenti in z. Alla fine di questo passo la riga i-esima non è più necessaria: si deve quindi eliminare il primo elemento di tutte le sotto-colonne memorizzate in z, compattando gli elementi rimasti, ed in più si devono memorizzare gli elementi i+1… n+1 della colonna i.
Un esempio renderà più chiaro lo schema di allocazione1: si supponga, per semplicità, che la matrice A sia 3× 3, quindi la matrice Z ha dimensioni 4× 3 ed il vettore deve essere dimensionato per contenere (n+1)2/4=42/4=4 elementi.
Al primo passo non si ha bisogno di elementi memorizzati in z, ma si dovranno solo memorizzare gli elementi della colonna corrente necessari in seguito:
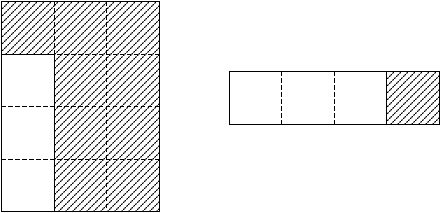
Figure 3.2: Contenuto di Z e z al termine del passo 1
Il passo 2 necessita degli elementi appena memorizzati per aggiornare la colonna corrente; questa verrà modificata ed si memorizzano gli elementi utili:
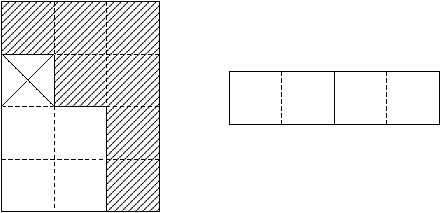
Figure 3.3: Contenuto di Z e z al termine del passo 2
Infine, alla terza ed ultima iterazione, dopo l’aggiornamento della colonna corrente e la memorizzazione degli elementi opportuni si avrà la seguente situazione:
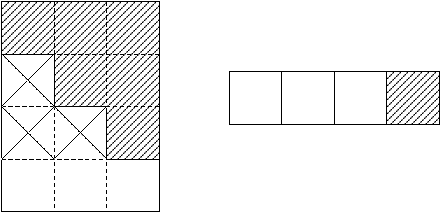
Figure 3.4: Contenuto di Z e z al termine del passo 3
dove l’ultima riga di Z e i primi n elementi di z contengono la soluzione cercata.
Un esempio maggiormente complesso è dato in figura ?? (di cui si mostrerà solo il contenuto del vettore z durante i vari passi):
Per accedere agli elementi di z si è usato il seguente schema: si supponga di essere al passo k e di dover accedere all’elemento di indici (i,j) (con i≥ k e j<k, per quanto visto in precedenza); si è visto che z contiene gli elementi di Z ordinati per colonne, ognuna delle quali contiene n−k+2 elementi: dal momento che per accedere alla prima colonna non si ha bisogno di un offset, in quanto questa si trova all’inizio di z, per ottenere l’indice dell’elemento precedente l’inizio della colonna j, si calcola offsetj=(n−k+2)(j−1). Ora, per accedere all’elemento (k+1,j) si deve incrementare di 1 offsetj ed allora per accedere all’elemento (i,j) si deve aggiungere la quantità i−k+1. In conclusione:
| Z[i,j] = z[ |
| + |
| ] | ||||||||||||||||||||||||||||||||||||
Frequentemente si ha la necessità di risolvere sistemi lineari in cui la matrice dei coefficienti rimane costante, ma dove il vettore dei termini noti cambia: è quindi di grande interesse poter risolvere in modo efficiente più sistemi lineari con la stessa matrice dei coefficienti ma con differenti termini noti, eseguendo la fattorizzazione della matrice solamente una volta.
Il problema, adesso, è il seguente: dato il sistema
| AX=B |
con A ∈ ℝn × n e X, B ∈ ℝn × m, determinare la matrice X che lo soddisfa.
Le colonne della matrice soluzione X, x(i), sono i vettori soluzione degli m sistemi lineari
| Ax(i) = b(i) i=1,…, m, |
uno per ogni vettore colonna b(i) della matrice dei termini noti.
L’applicazione del metodo di Wassing, in questo caso, cambia solo nella sua organizzazione. Idealmente, è come se la matrice Z adesso fosse strutturata in:
| Z= | ⎡ ⎢ ⎢ ⎣ |
| ⎤ ⎥ ⎥ ⎦ |
dove, al posto del precedente vettore −bT, si ha la matrice −BT.
In realtà, le matrici A e B sono mantenute separate; la prima nel vettore z, come mostrato in precedenza, la seconda in un altro vettore, b.
Siano m i vettori b(i), allora la matrice B viene riorganizzata nel vettore b come mostrato in figura ??: siano, cioè, Bi, i=1,…,n le n righe di B, allora esse saranno poste l’una di seguito l’altra nel vettore b.
Utilizzando questo metodo di allocazione, le operazioni di aggiornamento avvengono in maniera efficiente; gli elementi da modificare si trovano sulla stessa riga della matrice B: memorizzando in modo consecutivo questi elementi nel vettore b, l’accesso ad essi avverrà in maniera sequenziale, evitando perciò accessi non contigui in memoria.
Dal momento che l’algoritmo per più termini noti è più generale, le librerie implementate dispongono soltanto di questa versione. Per questo, il vettore z dovrà essere dimensionato per contenere n2/4 elementi, mentre il vettore b dovrà contenere mn elementi.
La gestione della memoria, ed in particolare dell’allocazione dei vettori, avviene con modalità differenti tra il Fortran ed il C.
Il Fortran prevede che i vettori necessari all’esecuzione delle subroutine siano dichiarati prima nel programma principale, per poi essere passati, come parametri, ai sottoprogrammi.
In C, invece, è possibile far uso di funzioni di allocazione dinamica della memoria per la dichiarazione dei vettori direttamente all’interno delle subroutine, senza percui aver bisogno di parametri aggiuntivi.
La tecnica del pivoting parziale consiste nello scambiare le righe della matrice in modo da posizionare un elemento particolarmente desiderabile nella posizione diagonale, dalla quale l’elemento pivot deve essere scelto.
Si è optato, allora, per usare la metodologia classica di scelta del pivot come l’elemento di modulo massimo nella colonna corrente. È noto, infatti, che questa strategia consente di ottenere un metodo numerico stabile.
Per l’applicazione del pivoting parziale vengono mantenuti due vettori (inizialmente contengono vect[i]=i):
Il motivo dell’uso di due vettori è il seguente: la scrittura degli elementi nel vettore z viene ordinata per mezzo del vettore ip, ed anche gli elementi delle colonne di Z, che vengono letti ed inseriti nel vettore c (vettore, appunto, che contiene la colonna corrente), sono ordinati per ip. Così facendo, il primo punto del secondo passo avviene senza far uso di vettori di indici. Quando poi si effettua la ricerca del pivot all’interno del ciclo su k, non si può più usare il vettore ip (che comunque viene aggiornato per i passi successivi), ma si ha bisogno di un altro vettore che tenga traccia solo dell’ultimo scambio di righe, in modo da poter applicare l’ultima permutazione anche agli elementi già ordinati per ip.
Gli scambi attuati dal pivoting avvengono sulle righe della matrice Z, scambiando quindi l’ordine degli elementi all’interno di una stessa colonna, ma senza che essi vengano scambiati tra colonne differenti. Dal momento che ogni elemento di b necessita, per essere aggiornato, di un’intera colonna di Z, le componenti del vettore b non devono essere permutate ad ogni iterazione. Risulta invece necessario ordinare detto vettore secondo ip alla fine dell’algoritmo, in quanto l’aver scambiato le righe di Z, la quale contiene AT, equivale ad aver scambiato le colonne di A e cioè l’ordine delle incognite nelle equazioni del sistema.
Il linguaggio C, al contrario del Fortran, non dispone dell’aritmetica dei numeri complessi: si è quindi dovuto ovviare a questa mancanza scrivendo delle routine opportune.
All’inizio, sono state utilizzate le funzioni disponibili nei Numerical Recipes (cfr. [, pg. 176-178, 948-950]), studiate appositamente per applicazioni numeriche in modo da ridurre possibili problemi dovuti all’aritmetica floating point.
Purtroppo, sebbene siano pensate per aumentare l’accuratezza dei calcoli, il fatto che debbano essere chiamate un numero considerevole di volte, porta ad un degrado inaccettabile delle prestazioni, a volte anche raddoppiando il tempo di esecuzione.
Il C, però, possiede un’interessante possibilità per ovviare a questo inconveniente: le macro del preprocessore (da ora chiamate solo macro); queste consentono di associare ad un nome una costante, un’istruzione o un insieme di istruzioni; nella fase precedente la compilazione, dove cioè interviene il preprocessore, tutte le occorrenze del nome di una macro vengono sostituite con il codice ad esso associato. L’utilizzo delle macro permette di mantenere il codice leggibile consentendo di svilupparlo modularmente, ma senza introdurre i rallentamenti dovuti alle chiamate a funzioni.
Poiché lo scopo non era quello di scrivere delle macro generali per le operazioni complesse ma solo quello di rendere efficienti i calcoli mantenendo il codice leggibile, si sono analizzate in dettaglio le operazioni che vengono svolte e si è notato come queste siano di tre tipi:
Si sono quindi modificate le routine citate in precedenza al fine di creare delle macro che svolgessero in un unico passo queste operazioni.
Oltre all’assenza dell’aritmetica complessa, il C è privo anche di una struttura dati primitiva per la gestione dei numeri complessi, per rappresentare i quali si è creato una struttura a due campi che contengano, rispettivamente, la parte reale e la parte immaginaria del numero.
Ancora nei Numerical Recipes viene indicata una strategia per la gestione in maniera efficiente di vettori di numeri complessi (cfr. [, pg. 24, 507-508]). Questa si basa sull’idea di gestire esplicitamente ogni numero complesso come parte reale e parte immaginaria (senza utilizzare strutture ausiliarie come struct), dichiarando un vettore di n complessi come un vettore di 2n numeri floating point, per poi idealmente utilizzare l’array come se fosse diviso in coppie che rappresentano, ciascuna, un numero complesso.
Sebbene venisse prospettato un incremento nelle prestazioni, esso non c’è stato, anzi, in alcuni casi, il metodo rivisto secondo queste indicazioni è risultato più lento di quello originario di circa il 10%. Si è mantenuta, pertanto, la versione senza queste modifiche.
Nella versione tradizionale del linguaggio C di Kernighan e Ritchie [], le variabili float sono automaticamente convertite al tipo double prima di ogni operazione, comprese quindi quelle aritmetiche ed il passaggio dei parametri a funzione. In questo modo tutta l’aritmetica è eseguita in doppia precisione: infatti, tutte le funzioni delle librerie standard C per le operazioni aritmetiche sono di tipo double e vengono quindi eseguite in doppia precisione. Nel caso in cui il risultato dell’operazione debba essere assegnato ad una variabile di tipo float, la precisione “in eccesso” viene scartata.
Questo comportamento non è più vero in generale, in quanto l’ANSI C [] stabilisce che l’aritmetica sugli operatori float può avvenire in singola precisione, invece che in doppia; dal momento che è solo una possibilità, spesso i compilatori fanno uso esclusivo dell’aritmetica in doppia precisione, se non specificato altrimenti.
Il modo di operare della prima edizione del C consente di semplificare l’architettura delle librerie standard, in quanto è necessario fornire una sola implementazione di ogni funzione, e solitamente un po’ di precisione in più non provoca alcun danno. Purtroppo, questa conversione automatica non consente di scrivere codici numerici efficienti, in quanto esiste una precisa ragione algoritmica per avere singola o doppia precisione, anche per una questione di massimizzazione delle performance: si vedano per esempio i grafici ?? e ?? del tempo di esecuzione delle routine per il metodo di Wassing con e senza le ottimizzazioni (-O3) attivate, le quali disabilitano la conversione automatica.
Si vede bene in figura ?? che i tempi delle routine utilizzanti la singola precisione sono molto simili a quelle che usano la doppia precisione. Al contrario, in figura ?? i tempi risultano coerenti con le aspettative, ovvero, i tempi di esecuzione in singola precisione sono approssimativamente dimezzati, rispetto alle analoghe in doppia precisione.
Ove possibile, si consiglia di eliminare la conversione automatica in quanto un codice scritto per la singola precisione risulta essere lento quasi quanto uno scritto in doppia precisione, ma con una accuratezza nettamente minore.
Si usano ancora le figure ?? e ?? per mostrare una importante caratteristica del compilatore gcc/g77: si noti, infatti, il miglioramento notevole delle prestazioni (anche del 50%) attivando l’ottimizzazione -O3 del compilatore (esistono diversi livelli di ottimizzazione, per approfondimenti si consulti man gcc).
Le ottimizzazioni -Ox, con x=1, 2, 3, raggruppano diverse opzioni di compilazione rivolte principalmente a migliorare le prestazioni nella gestione della memoria, nell’esecuzione di operazioni matematiche e nell’ordine di esecuzione delle istruzioni all’interno del programma. La meno aggressiva delle tre è -O1, mentre quella che consente i maggiori guadagni, a fronte di un tempo di compilazione maggiore, è -O3 (l’opzione utilizzata per tutti i test svolti).
L’utilizzo delle ottimizzazione è vivamente consigliato, in quanto con lo stesso codice sorgente vengono generati eseguibili più performanti. Tuttavia, questo è raccomandabile soltanto ad un punto dello sviluppo ormai maturo: infatti, il guadagno ottenibile potrebbe mascherare parti di codice poco efficienti, che invece potrebbero essere identificate senza l’utilizzo delle ottimizzazioni.
Esaminiamo ora la complessità del metodo di Wassing e quindi quali prestazioni ci si possono attendere; nel far questo verranno prese in considerazione solo le operazioni floating point, in quanto molto più lente di quelle tra interi.
Riguardando alla descrizione del metodo della sezione ??, si può notare come la parte che contribuisce maggiormente alla complessità dell’algoritmo è principalmente la 2), in quanto l’ultimo passo non introduce praticamente nessuna operazione di rilievo, mentre nel punto 1) vengono eseguite n operazioni2 dovute alle divisioni necessarie alla modifica della prima colonna, del tutto trascurabili rispetto alle operazioni della 2)
Analizziamo dunque in dettaglio questa sezione, esaminando i vari passi che lo compongono:
zik=zik + ∑j=1k−1 zijzjk
Si eseguono n−k+2 somme per modificare gli elementi zik aggiungendovi la sommatoria, la quale richiede k−2 somme e k−1 moltiplicazioni, per un totale di (n−k+2)(2k−3+1)=(n−k+2)(2k−2) operazioni.
zik=−zik/zkk
Per modificare un elemento si ha bisogno di eseguire una sola operazione, la divisione. Si ha dunque un totale di (n−k+1) operazioni per l’aggiornamento degli altrettanti elementi.
zij=zij + zikzkj
Si eseguono due operazioni per aggiornare ogni elemento che si trova nella sotto-matrice di indici (i,j)=(k+1… n+1, 1… k−1); sono pertanto necessarie 2(k−1)(n−k+1) operazioni per completare l’aggiornamento.
I tre punti analizzati in precedenza, si trovano all’interno di un ciclo su k che varia tra 2 ed n; si dovranno dunque sommare questi contributi al variare di k (alcuni termini verranno omessi in quanto non contribuiscono a determinare la complessità dell’algoritmo ed i passaggi fra un’equazione e la successiva non avranno il simbolo di uguaglianza ma quello di approssimazione):
|
Nel caso l’algoritmo utilizzato faccia uso del pivoting parziale, si devono anche considerare i confronti, che hanno costo proporzionale a O(n2), mentre in caso non si faccia uso del pivoting i confronti sono proporzionali a O(n).
La complessità risulta essere, pertanto, identica a quella del metodo di eliminazione di Gauss, con eventuale pivoting. Alle stesse conclusioni si perviene nel caso di più termini noti, ovvero, se si hanno m termini noti, allora si ottiene una complessità di
| n3+2mn2 |
flops.


