Chapter 4 Sperimentazione e risultati

Il metodo di Wassing è stato implementato:

con e senza pivoting;
in singola e doppia precisione;
in aritmetica reale e complessa;
in linguaggio Fortran e C.

Le routine sviluppate sono state confrontate con le omologhe routine LAPACK [] [], che è la libreria standard di comune utilizzo per le applicazioni scientifiche ed industriali, nelle quali sia richiesta la risoluzione di sistemi lineari a matrice densa.

4.1 Piattaforma hardware

Il computer su cui sono stati eseguiti tutti i test ha le seguenti caratteristiche:

Processore:: Pentium4 1.8GHz, 512KB cache;
Memoria:: 512MB;
S.O.:: Gentoo GNU/Linux, kernel 2.4.20-gentoo-r6;
gcc/g77:: versione 3.2.3 20030422;
glibc:: versione 2.3.2-r3;
Librerie LAPACK:: versione 3.0;

presso il Centro di Calcolo del Dipartimento di Matematica “Ulisse Dini”.

4.2 Sistemi lineari di test

Verranno ora descritti i sistemi lineari utilizzati nei test delle performance e sull’accuratezza.

Come evidenziato in maggior dettaglio nella sezione ??, verrà presa in considerazione la matrice A^T e non direttamente A, matrice dei coefficienti del sistema lineare.

La matrice utilizzata nel caso di numeri reali è la matrice di Hilbert con la diagonale principale incrementata di 1:

i = j

→

a_ij = 1+

i+j−1

i ≠ j

→

a_ij =

i+j−1

Questa matrice è a diagonale dominante (oltre che simmetrica e definita positiva) e risulta ben condizionata, come si vede in figura ??.

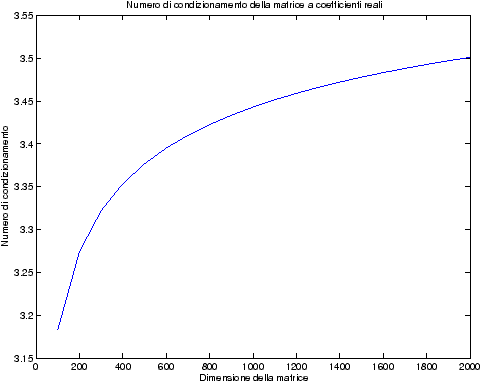
Figure 4.1: Numero di condizionamento per la matrice a coefficienti reali

La matrice viene utilizzata nel caso di numeri reali per i test di performance ed in quelli di accuratezza che non implementano il pivoting.

Nel caso di numeri complessi¹, la precedente matrice viene modificata in modo opportuno:

i = j

→

a_ij =

⎛
⎜
⎝

i+j−1

, 0

⎞
⎟
⎠

i < j

→

a_ij =

⎛
⎜
⎝

i+j−1

⎞
⎟
⎠

i > j

→

a_ij =

⎛
⎜
⎝

0, −

i+j−1

⎞
⎟
⎠

Il numero di condizionamento di questa matrice, mostrato in figura ??, è basso, indice di come essa sia ben condizionata.

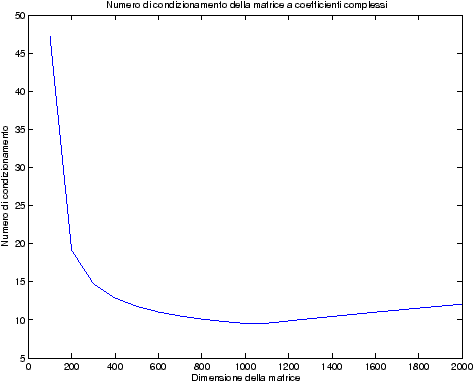
Figure 4.2: Numero di condizionamento per la matrice a coefficienti complessi

Per verificare l’accuratezza dei metodi con pivoting parziale, sono state utilizzate le seguenti matrici:

numeri reali:
i+j = n+1 →
a_ij = 1+
1

n−i+j

else →
a_ij =
1

n−i+j
numeri complessi:
i+j = n+1 →
a_ij = ⎛
⎜
⎝ 1+
1

n−i+j

,  0 ⎞
⎟
⎠

i+j ≤ n →
a_ij = ⎛
⎜
⎝ 0,  −
1

n−i+j

⎞
⎟
⎠

else →
a_ij = ⎛
⎜
⎝ 0,
1

n−i+j

⎞
⎟
⎠

Queste matrici sono ottenute dalle precedenti invertendo l’ordine delle righe: la prima diventa l’ultima, la seconda la penultima, e così via; le matrici sono antidiagonali dominanti ed è quindi necessario applicare il pivoting per ottenere dei risultati corretti.

Il termine noto, per i test di performance, non è particolarmente importate, ed il vettore b è stato scelto come composto da tutti 3 per i numeri reali, e da (3,0) per i numeri complessi.

Per i test di accuratezza, invece, la scelta del termine noto diventa più importante: ogni elemento del vettore b è stato scelto come la somma degli elementi sulla riga omologa della matrice dei coefficienti, in modo tale, pertanto, da avere, come soluzione, il vettore x=(1,…,1)^T.

4.3 Modalità dei confronti

I test eseguiti sono suddivisi in due categorie:

test delle performance;
test sull’accuratezza.

I codici sono stati tutti compilati attivando le ottimizzazioni di compilazione -O3 e la generazione, l’esecuzione e l’analisi dei risultati dei test sono state automatizzate tramite l’utilizzo di alcuni script.

Per i test delle performance, l’algoritmo che implementa il metodo di Wassing con pivoting viene confrontato con la routine LAPACK di risoluzione di sistemi lineari generali, gesv. Gli algoritmi senza pivoting, invece, sono stati confrontati, oltre che con gesv, anche con la routine per sistemi lineari con la matrice dei coefficienti simmetrica e definita positiva posv che, tuttavia, ha una complessità di 1/3n³ flops, invece che 2/3n³. I test con le funzioni posv di LAPACK sono state svolte solo per numeri reali, in quanto la matrice complessa utilizzata non è definita positiva per n≥ 68.

I test sull’accuratezza confrontano i metodi con e senza pivoting con la routine LAPACK gesv; viene poi confrontata l’accuratezza delle implementazioni in Fortran e C.

4.4 Test delle performance

Dal momento che l’obiettivo principale dell’algoritmo è il risparmio di memoria, è prevedibile una riduzione della velocità di esecuzione rispetto a metodi classici come l’eliminazione di Gauss.

Per stimare questa perdita si è confrontato la velocità di esecuzione del metodo di Wassing in relazione ad analoghe routine LAPACK: si è fatta variare la dimensione del sistema da risolvere tra n=250 ed n=2000 con incrementi di 250. Ogni esecuzione è stata ripetuta 30 volte e dei tempi viene presa la media, per cercare di ridurre l’influenza di eventuali altri programmi e/o servizi in quel momento in esecuzione.

Dal momento che l’algoritmo implementato consente la risoluzione simultanea di più sistemi lineari aventi la stessa matrice dei coefficienti, si sono volute stimare le performance anche in questo caso.

Il numero di termini noti, nb, è stato fatto variare come nb=5, 10, 15, …, 50, mentre la dimensione del sistema è mantenuta costante, e pari a n=2000, in modo da avere differenze più marcate nei tempi con differenti valori di nb. Anche in questo caso, le esecuzioni sono state eseguite 30 volte, prendendo poi la media dei tempi.

Per monitorare il tempo di esecuzione si è utilizzato l’utility time (anche se è stato necessario ricompilarla, in quanto quella disponibile sul sistema di test dava alcuni problemi). La scelta di utilizzare un programma esterno, rispetto alle istruzioni messe a disposizione dal Fortran e dal C, è stata fatta per evitare che metodi differenti di acquisizione del tempo da parte dei due linguaggi avessero ripercussioni sull’analisi a-posteriori dei risultati.

4.4.1 Analisi dei risultati

I grafici vengono presentati in tabelle di quattro immagini, in modo da poter raggruppare le presentazioni in maniera organica: le figure sono infatti riunite al variare del tipo di dato, del linguaggio di programmazione e delle routine impiegate. Lo schema di presentazione è il seguente:

tab. ??-??:: tempi di esecuzioni della routine per il metodo di Wassing e LAPACK, in Fortran e C: ogni grafico mostra i tempi di esecuzione al variare del tipo di dato;
tab. ??-??:: confronto dei tempi di esecuzione delle routine per il metodo di Wassing nelle implementazioni Fortran e C: ogni grafico mostra i tempi di esecuzione delle due implementazioni, divisi per tipo di dato, con e senza pivoting;
tab. ??-??:: confronti tra il metodo di Wassing, con e senza pivoting, con le routine LAPACK corrispondenti, in Fortran e C;
tab. ??:: rapporto dei tempi di esecuzioni del metodo di Wassing e delle routine LAPACK nelle implementazioni in Fortran e C;
tab. ??-??:: confronto dei tempi di esecuzioni delle routine LAPACK nelle implementazioni in Fortran e C;
tab. ??..??:: confronto dei tempi di esecuzione del metodo di Wassing e delle routine LAPACK nel caso di più termini noti.

Come ci si poteva aspettare, il tempo di esecuzione delle routine LAPACK non cambia nelle due implementazioni (tabelle ?? e ??).

Più interessante è osservare il comportamento delle routine per il metodo di Wassing in Fortran e C: mentre per la doppia precisione i tempi sono praticamente uguali (sebbene il C risulti leggermente più lento), lo stesso non è più vero per la singola precisione. Questo comportamento è evidente nelle tabelle ?? e ??, ed ancora più chiaramente in tabella ??. Si può notare, a titolo di esempio, come l’implementazione C per i numeri complessi in singola precisione risulti essere meno performante (attorno al 20%) rispetto a quella Fortran: questo può essere dovuto all’assenza dell’aritmetica complessa in C, cui si è sopperito tramite funzioni aggiuntive. Questa differenza viene meno nel caso di doppia precisione, forse anche per la maggior lentezza di esecuzione di queste operazioni.

Nel caso di più termini noti, al crescere del loro numero, il tempo di esecuzione aumenta di conseguenza anche se, come era prevedibile, la parte che maggiormente contribuisce alle performance rimane quella di fattorizzazione della matrice. Inoltre, si può notare in tabella ?? come, al crescere del numero di termini noti nel sistema, le prestazioni del metodo di Wassing e delle routine LAPACK tendano ad avvicinarsi, anche se lentamente.

Infine, nelle tabelle ?? e ?? si ha il confronto di prestazioni tra il metodo implementato e le routine LAPACK. Come ci si attendeva, le prestazioni del codice per il metodo di Wassing risultano minori di quelle LAPACK, a causa dei maggiori spostamenti dei dati in memoria. Tuttavia, la perdita di prestazioni, che è al massimo del 50%, viene controbilanciata da un utilizzo 4 volte inferiore di memoria.

4.5 Verifica dell’accuratezza

L’accuratezza di un codice di calcolo è uno dei suoi aspetti fondamentali. Talora è preferibile utilizzare uno strumento che necessiti di un maggior tempo di esecuzione ma che garantisca una maggiore accuratezza dei risultati. È dunque necessario verificare l’accuratezza dei codici su problemi test opportuni.

L’accuratezza che possiamo ottenere nella risoluzione di un sistema lineare

Ax=b

dipende dal numero di condizionamento, κ(A), della matrice A. A parità di numero di condizionamento (ovvero di problema da risolvere) è quindi interessante confrontare l’accuratezza ottenuta con i vari codici.

Per far questo si hanno a disposizione due possibilità: studiare l’errore (err=x−x) oppure studiare il residuo (r=b−Ax); la seconda opzione è stata scartata in quanto presenta due problemi, uno di carattere teorico (è possibile avere un residuo “piccolo” con un errore molto grande, cfr. [, pg. 181] [] []) ed uno di carattere pratico (è necessario eseguire esplicitamente il prodotto tra la matrice dei coefficienti e la soluzione calcolata e questo potrebbe introdurre ulteriori errori). Si è dunque optato per l’analisi dell’errore err.

Ottenuta dunque la soluzione x tramite il metodo numerico, è possibile valutare il corrispondente vettore di errore err=x−x. Calcolando, allora, ||err||₂=||x−x||₂ si ottiene una misura dell’errore commesso durante la risoluzione.

Sebbene ci si aspetti che le componenti del vettore err siano piccole, al crescere della dimensione del vettore, anche ||err||₂ tenderà a crescere di conseguenza (è infatti una somma di quantità non negative), rendendo difficile un confronto al variare della dimensione del sistema; per ovviare a questo inconveniente si è presa in considerazione un’altra quantità:

√

∑

i=1

err_i²

||err||₂

√

che normalizza la misura dell’errore, in relazione alla dimensione del problema (cfr. [, pg. 86]), ed a cui si farà riferimento in seguito col nome di norma 2 “pesata”.

Oltre a questo indicatore, si è anche voluto stimare l’errore massimo commesso durante la risoluzione del sistema lineare, cioè il più grande scostamento di una componente di x dall’omologa componente del vettore x:

max

i=1,…,n

|x_i−x_i| = ||err||_∞.

4.5.1 Analisi dei risultati

Le modalità di rappresentazione dei risultati sono simili a quanto già visto nella sezione ??: i grafici sono raggruppati in gruppi di quattro, al variare del tipo di dato. Viene mostrata la norma 2 “pesata” e la norma infinito del metodo di Wassing in tutte le varianti implementate, confrontandole sia tra di loro, che con le analoghe routine LAPACK. La presentazione avviene in quest’ordine:

tab. ??-??:: Fortran, confronto di norma 2 e norma infinito tra il metodo di Wassing senza pivoting e la routine LAPACK gesv;
tab. ??-??:: Fortran, confronto di norma 2 e norma infinito tra il metodo di Wassing con pivoting e la routine LAPACK gesv;
tab. ??-??:: C, confronto di norma 2 e norma infinito tra il metodo di Wassing senza pivoting e la routine LAPACK gesv;
tab. ??-??:: C, confronto di norma 2 e norma infinito tra il metodo di Wassing con pivoting e la routine LAPACK gesv;
tab. ??..??:: confronto tra le implementazioni Fortran e C del metodo di Wassing senza pivoting e routine LAPACK gesv;
tab. ??..??:: confronto tra le implementazioni Fortran e C del metodo di Wassing con pivoting e routine LAPACK gesv;

Un fatto molto importante da notare è la quasi assoluta coincidenza dei risultati, riguardo all’accuratezza, del metodo di Wassing nei due linguaggi utilizzati (tant’è che si era pensato di proporre soltanto i risultati di un’implementazione e quelli di confronto): nel caso dei numeri reali, i grafici sono perfettamente sovrapponibili in tutti i casi analizzati, mentre per i numeri complessi le differenze sono più evidenti nel caso di utilizzo dell’algoritmo con pivoting (tabelle ?? e ??) rispetto a quello senza (tabelle ?? e ??).

La precisione delle routine LAPACK, come ci si poteva attendere, rimane la stessa nel linguaggio Fortran e C; le librerie, infatti, sono sì scritte in Fortran, ma sono già compilate, quindi nei due linguaggi si fa uso della stessa identica routine.

Di particolare interesse è il confronto tra la precisione del metodo di Wassing e delle routine LAPACK nel risolvere il medesimo problema. In generale, l’accuratezza risulta essere simile, eccezion fatta nel caso di numeri complessi negli algoritmi che implementano il pivoting: la routine gesv risulta, infatti, essere più precisa di circa una cifra decimale.

Table 4.1: Tempi di esecuzione delle routine wa[pvt]sv, Fortran e C

Table 4.2: Tempi di esecuzione delle routine LAPACK gesv e posv

Table 4.3: Confronto wasv Fortran e C

Table 4.4: Confronto wapvtsv Fortran e C

Table 4.5: Fortran, Confronti tra wasv, wapsvsv, gesv e posv

Table 4.6: C, Confronti tra wasv, wapsvsv, gesv e posv

Table 4.7: Rapporto dei tempi di esecuzione in Fortran e C delle routine utilizzate

Table 4.8: Confronti gesv in Fortran e C

Table 4.9: Confronti posv in Fortran e C e rapporto tra gesv e posv

Table 4.10: Più termini noti, Fortran, Confronto tra wapvtsv e gesv

Table 4.11: Più termini noti, C, Confronto tra wapvtsv e gesv

Table 4.12: Più termini noti, Rapporto tra wapvtsv e gesv

Table 4.13: Precisione, Fortran, Confronto norma 2 “pesata” wasv e gesv

Table 4.14: Precisione, Fortran, Confronto norma infinito wasv e gesv

Table 4.15: Precisione, Fortran, Confronto norma 2 “pesata” wapvtsv e gesv

Table 4.16: Precisione, Fortran, Confronto norma infinito wapvtsv e gesv

Table 4.17: Precisione, C, Confronto norma 2 “pesata” wasv e gesv

Table 4.18: Precisione, C, Confronto norma infinito wasv e gesv

Table 4.19: Precisione, C, Confronto norma 2 “pesata” wapvtsv e gesv

Table 4.20: Precisione, C, Confronto norma infinito wapvtsv e gesv

Table 4.21: Precisione, Confronto norma 2 “pesata” wasv, Fortran e C

Table 4.22: Precisione, Confronto norma 2 “pesata” gesv, Fortran e C

Table 4.23: Precisione, Confronto norma infinito wasv, Fortran e C

Table 4.24: Precisione, Confronto norma infinito gesv, Fortran e C

Table 4.25: Precisione, Pvt, Confronto norma 2 “pesata” wasv, Fortran e C

Table 4.26: Precisione, Pvt, Confronto norma 2 “pesata” gesv, Fortran e C

Table 4.27: Precisione, Pvt, Confronto norma infinito wasv, Fortran e C

Table 4.28: Precisione, Pvt, Confronto norma infinito gesv, Fortran e C

1: Per rappresentare i numeri complessi si utilizzerà la forma (a,b) ≡ z=a+ib, una coppia di numeri il cui primo elemento è la parte reale e il secondo la parte immaginaria.