Ottenere matrici simmetriche e definite positive

Vediamo come si può ottenere una matrice simmetrica e definita positiva: sia $B$ una matrice non singolare, allora $A=BB^T$ è una matrice simmetrica e definita positiva. Infatti $BB^T$ è simmetrica per costruzione e preso $v \neq \underline{0}$:

$$v^TAv=v^TBB^Tv=(v^TB)(B^Tv)$$

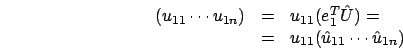detto ora $w=B^Tv$ abbiamo che $w \neq \underline{0}$ ed inoltre $w^T=v^TB$ possiamo allora scrivere

$$(v^TB)(B^Tv)=w^Tw= {\Vert w \Vert}_2^2 >0$$

poiche il vettore $w$ è non-nullo, ed è la condizione che cercavamo.

Per le matrici simmetriche e definite positive esiste anche una fattorizzazione, che non vedremo, come $RR^T$ dove con $R$ indichiamo una matrice triangolare inferiore; questa fattorizzazione ci sarà utile per la costruzione di una matrice simmetrica e definita positiva da utilizzare per le sperimentazioni del prossimo metodo.